Bài 11
a) Do c ⊥ a
c ⊥ b
=> a // b
b) Do a // b
=> ∠A₁ = ∠B₁ = 75⁰ (đồng vị)
=> ∠A₃ = ∠A₁ = 75⁰ (đồng vị)
Ta có:
∠A₄ + ∠A₃ = 180⁰ (kề bù)
=> ∠A₄ = 180⁰ - ∠A₃
= 180⁰ - 75⁰
= 105⁰
Bài 11:
a: a\(\perp\)c
b\(\perp\)c
Do đó: a//b
b: ta có: a//b
=>\(\widehat{A_3}=\widehat{B_1}\)(hai góc so le trong)
=>\(\widehat{A_3}=75^0\)
Ta có: \(\widehat{A_3}+\widehat{A_4}=180^0\)(hai góc kề bù)
=>\(\widehat{A_4}=180^0-75^0=105^0\)
Ta có: \(\widehat{A_3}=\widehat{A_1}\)(hai góc đối đỉnh)
mà \(\widehat{A_3}=75^0\)
nên \(\widehat{A_1}=75^0\)
Bài 12:
Gọi Bm là tia đối của tia BC
Ta có: \(\widehat{B_4}=\widehat{dBm}\)(hai góc đối đỉnh)
mà \(\widehat{dBm}=100^0\)
nên \(\widehat{B_4}=100^0\)
Ta có: d//d'
=>\(\widehat{B_4}=\widehat{C_2}\)(hai góc so le trong)
=>\(\widehat{C_2}=100^0\)
Ta có: \(\widehat{C_2}+\widehat{C_3}=180^0\)(hai góc kề bù)
=>\(\widehat{C_3}=180^0-100^0=80^0\)
Gọi An là tia đối của tia AB
Theo đề, ta có: \(\widehat{nAD}=61^0\)
Ta có: d//d'
=>\(\widehat{nAD}=\widehat{ADC}\)(hai góc so le trong)
=>\(\widehat{ADC}=61^0\)
Bài 13:
a: Ta có: a//b
a\(\perp\)c
Do đó: b\(\perp\)c
b: ta có: \(\widehat{D_1}=\widehat{ADC}\)(hai góc đối đỉnh)
mà \(\widehat{D_1}=55^0\)
nên \(\widehat{ADC}=55^0\)
Ta có: AD//CB
=>\(\widehat{ADC}+\widehat{BCD}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{BCD}=180^0-55^0=125^0\)

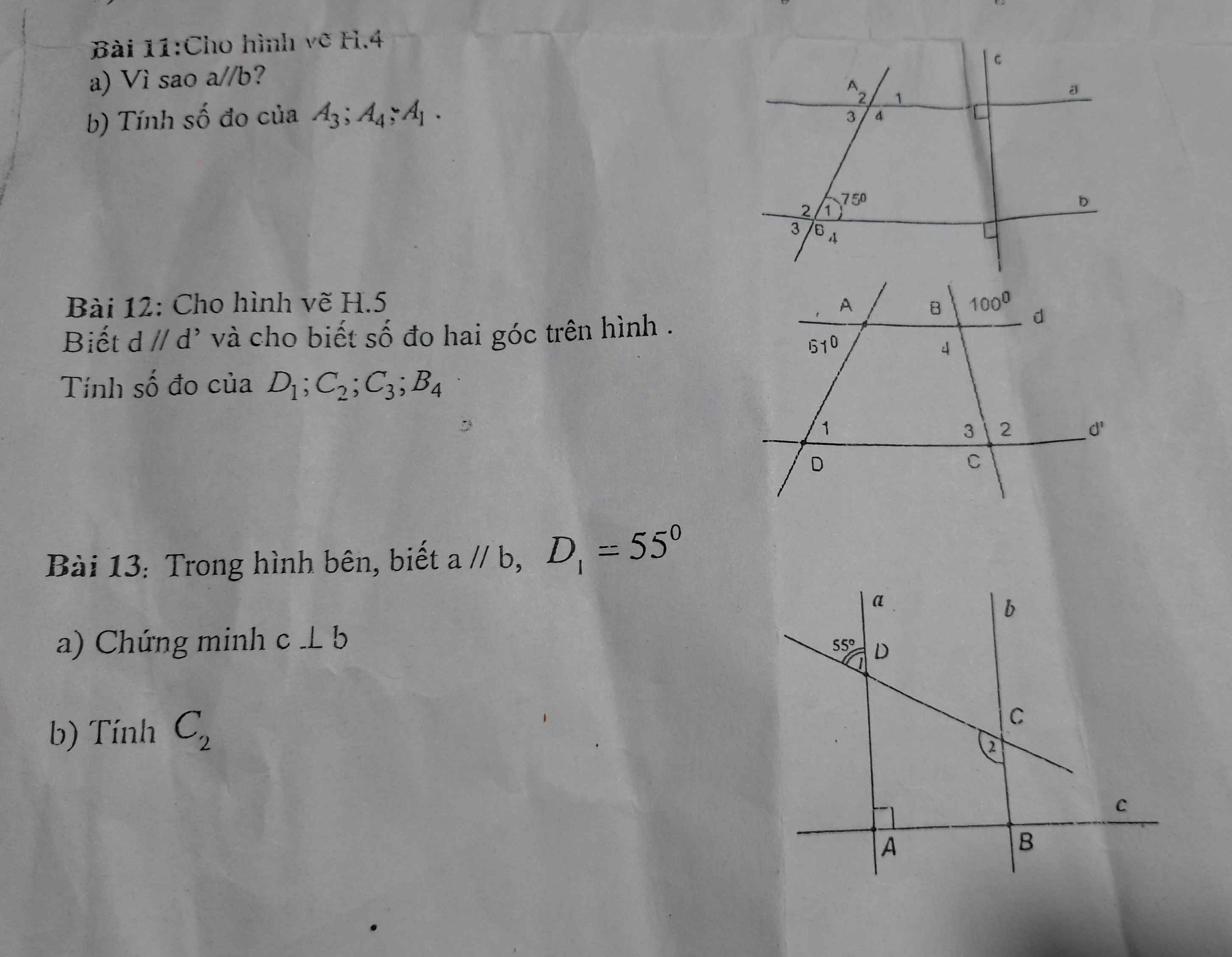



















 giúp tớ với mai tớ nộp rồi làm câu b và c cux đc ạ.
giúp tớ với mai tớ nộp rồi làm câu b và c cux đc ạ.