Question

giúp mình với ạ

Answer 1

`A = sin^2 25^o + sin^2 35^o + sin^2 55^o + sin^2 65^o`

`= ( sin^2 35^o + sin^2 55^o) + (sin^2 65^o+ sin^2 25^o)`

`= ( sin^2 35^o + cos^2 35^o) + (cos^2 25^o+ sin^2 25^o)`

`= 1 + 1`

`= 2`

`B = cot 20^o . cot 40^o . cot 50^o . cot 70^o`

`=  (cot 20^o . cot 70^o) . (cot 40^o . cot 50^o)`

`= (cot 20^o . tan 20^o) . (tan 50^o . cot 50^o)`

`= 1 . 1`

`= 1`

 

Answer 2

Bài 1:

a: 

\(A=sin^225^0+sin^235^0+sin^255^0+sin^265^0\)

\(=\left(sin^225^0+sin^265^0\right)+\left(sin^235^0+sin^255^0\right)\)

\(=\left(sin^225^0+cos^225^0\right)+\left(sin^235^0+cos^235^0\right)\)

=1+1=2

\(B=cot20^0\cdot cot40^0\cdot cot50^0\cdot cot70^0\)

\(=cot20^0\cdot tan20^0\cdot tan50^0\cdot cot50^0\)

\(=1\cdot1=1\)

b: Vẽ lại hình:

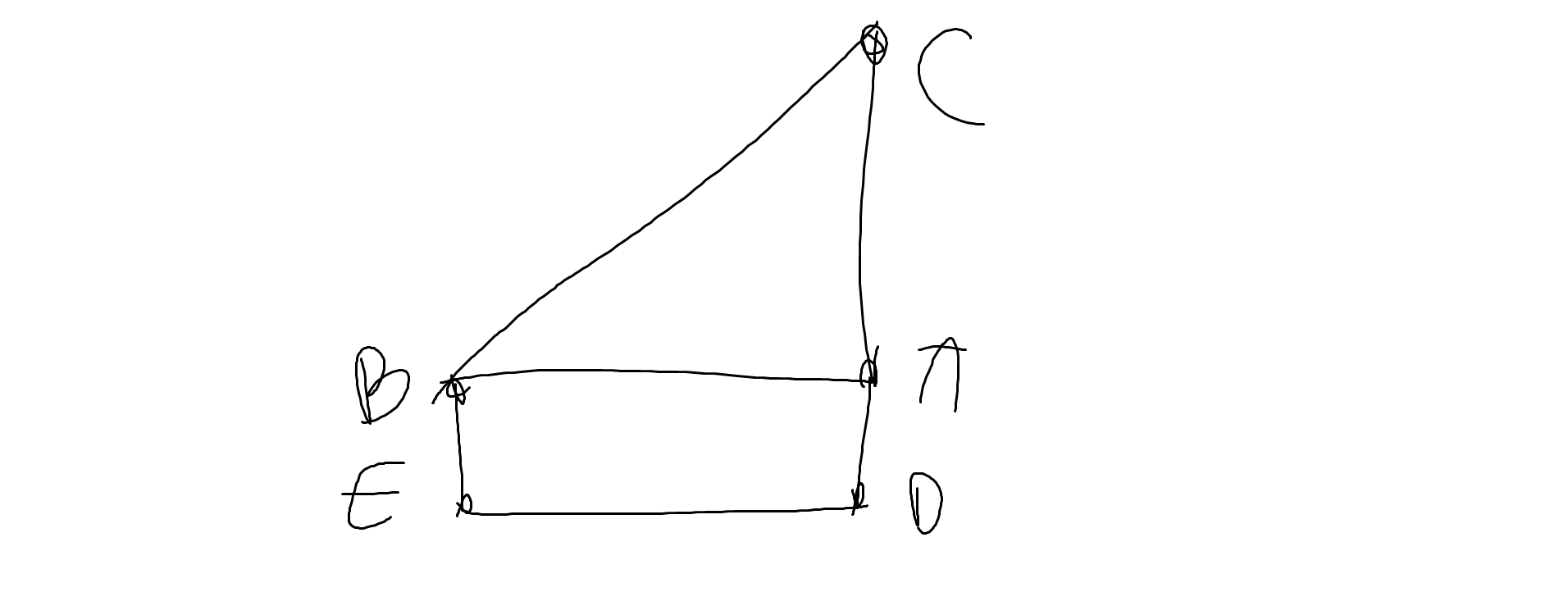
Xét ΔCAB vuông tại A có \(CA=AB\cdot tanABC\)

=>\(CA=20\cdot tan35\simeq14\left(m\right)\)

Chiều cao của cây là:

14+1,7=15,7(m)

 

Bài 2: Xét (K) có

ΔMOI nội tiếp

OI là đường kính

Do đó: ΔMOI vuông tại M

Xét (O) có

OM là bán kính

IM\(\perp\)MO tại M

Do đó: IM là tiếp tuyến của (M)