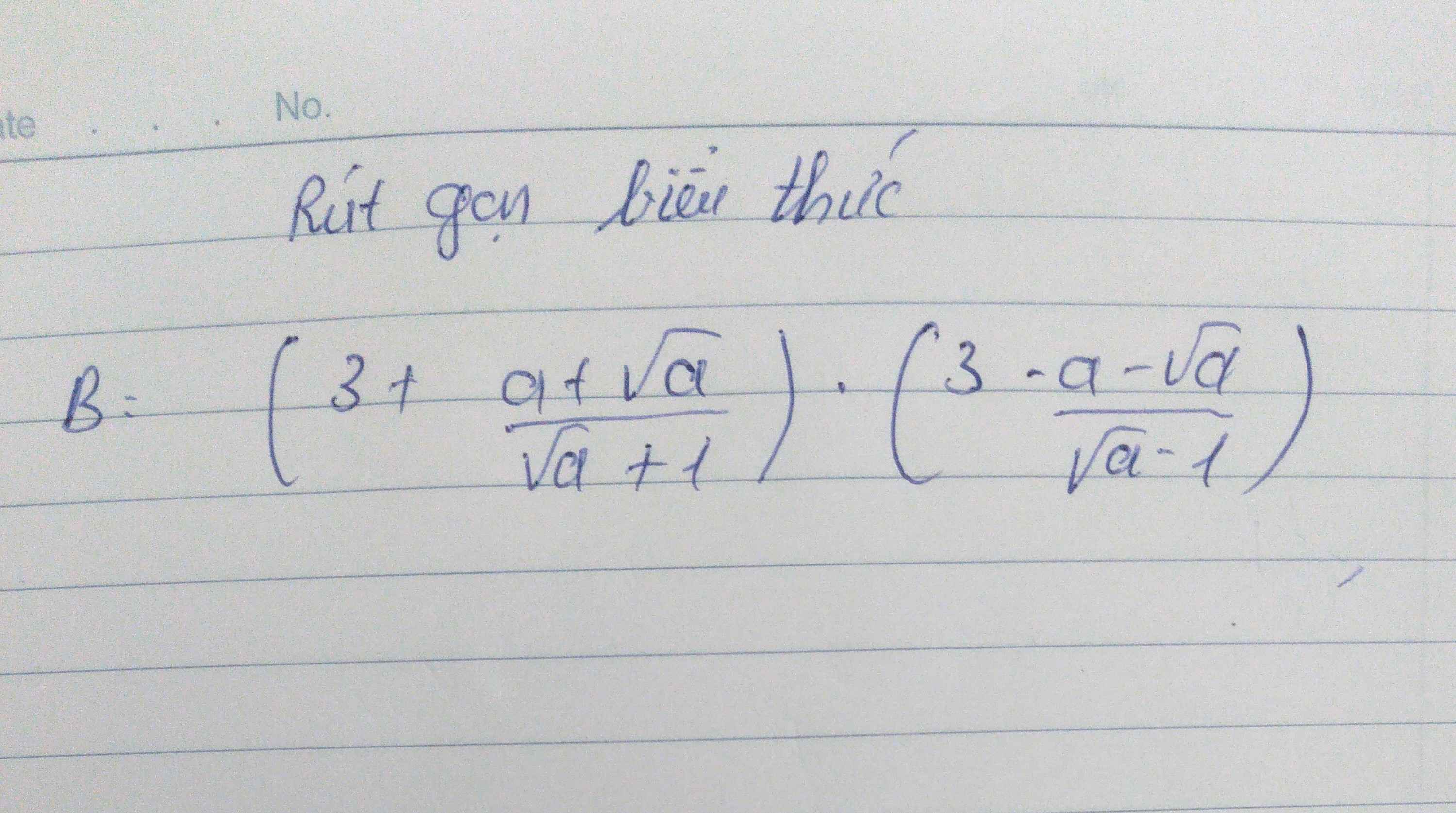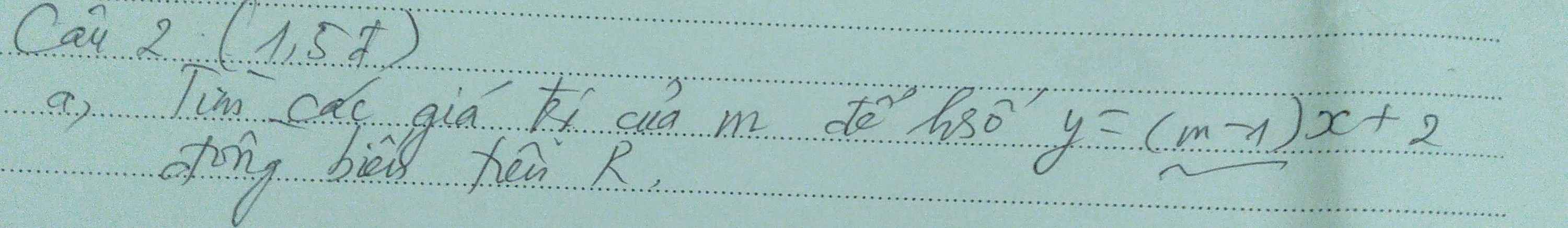\(B=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(3+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right)\left(3-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)=9-a\)
Để hàm số \(y=\left(m-1\right)x+2\) đồng biến trên R thì \(m-1>0\Rightarrow m>1\)
Câu 2:
Để hàm số y=(m-1)x+2 đồng biến trên R thì m-1>0
hay m>1
Câu 1:
Ta có: \(B=\left(3+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(3-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(=\left(3+\sqrt{a}\right)\left(3-\sqrt{a}\right)\)
=9-a