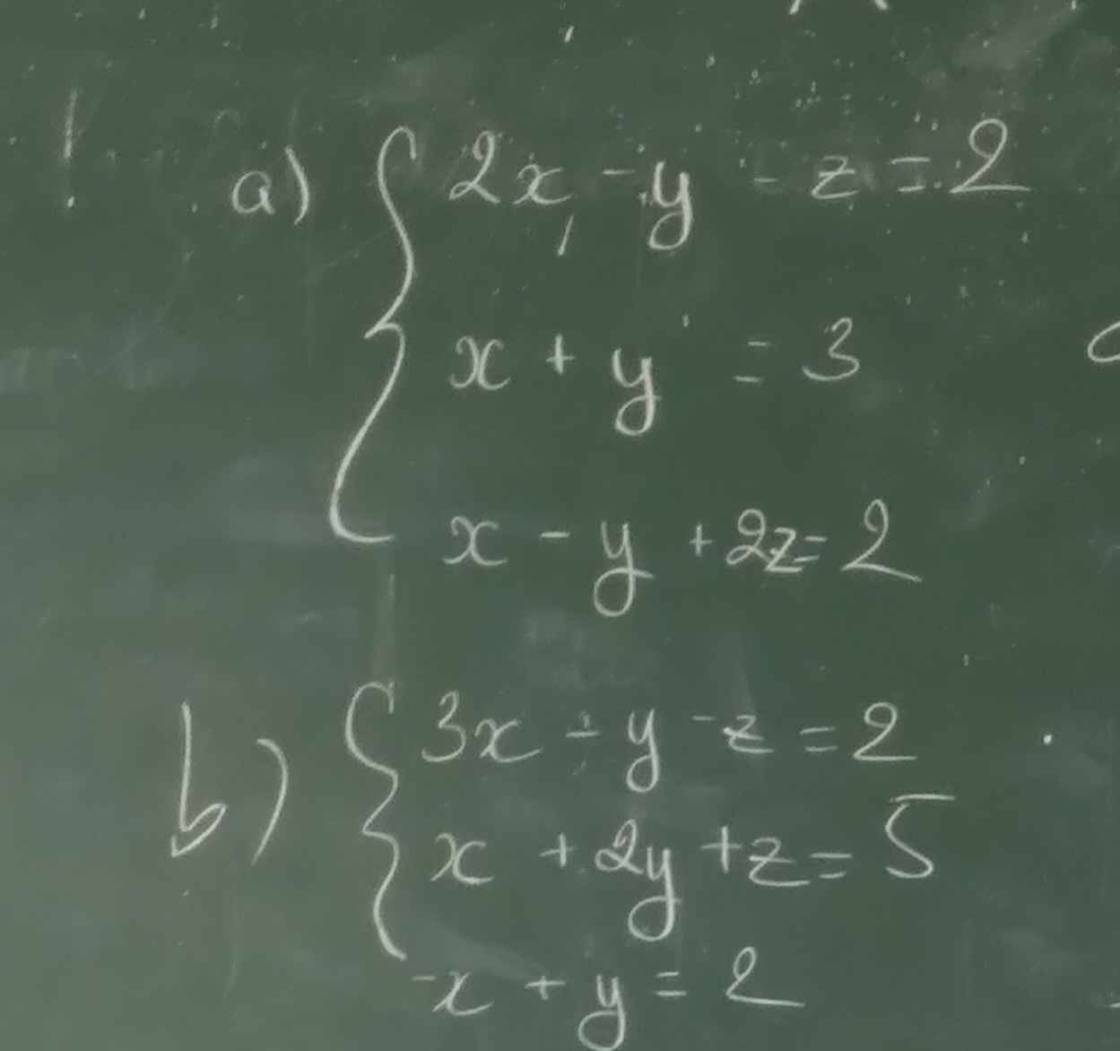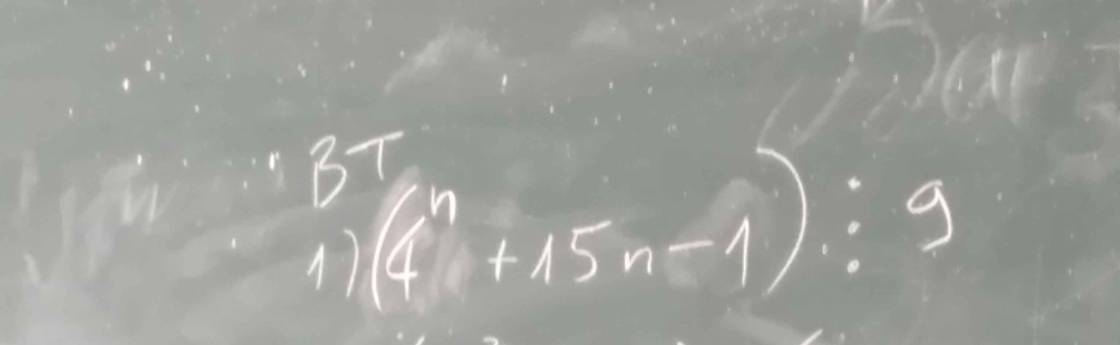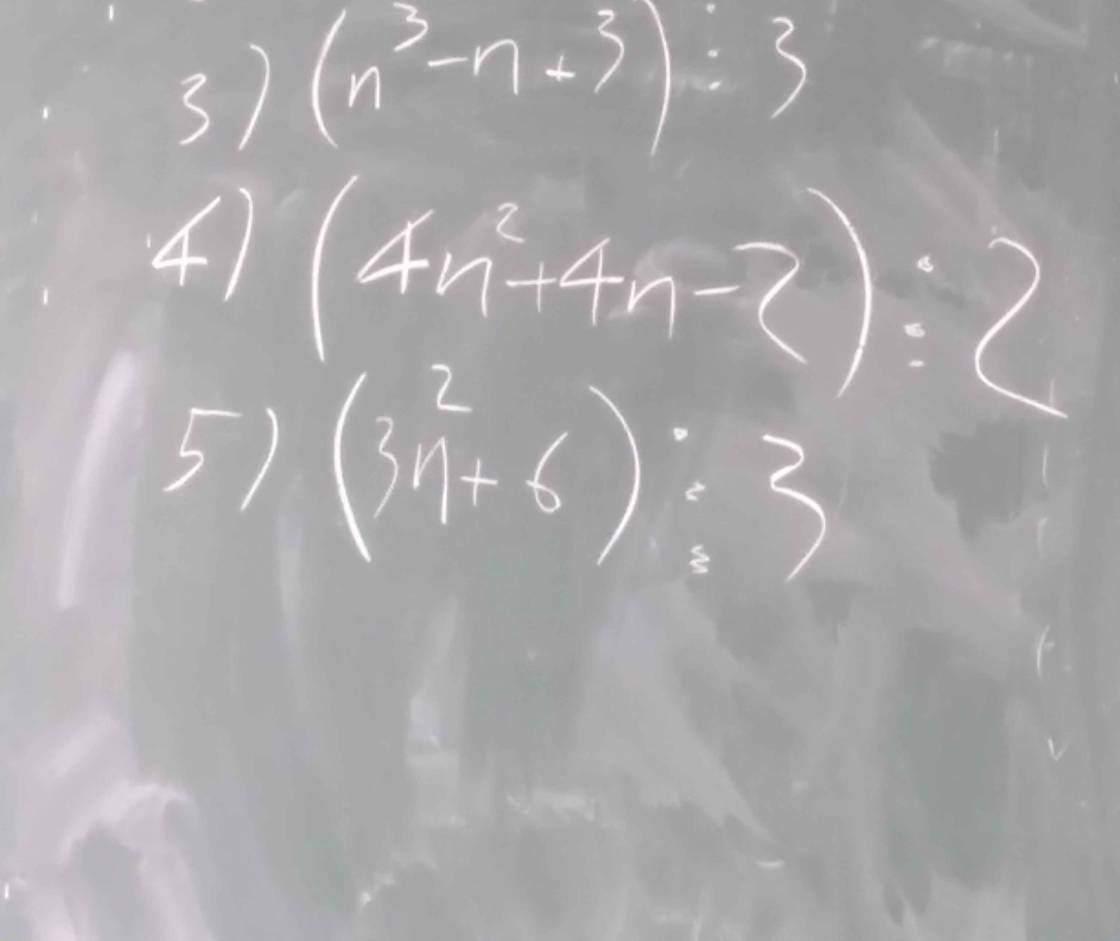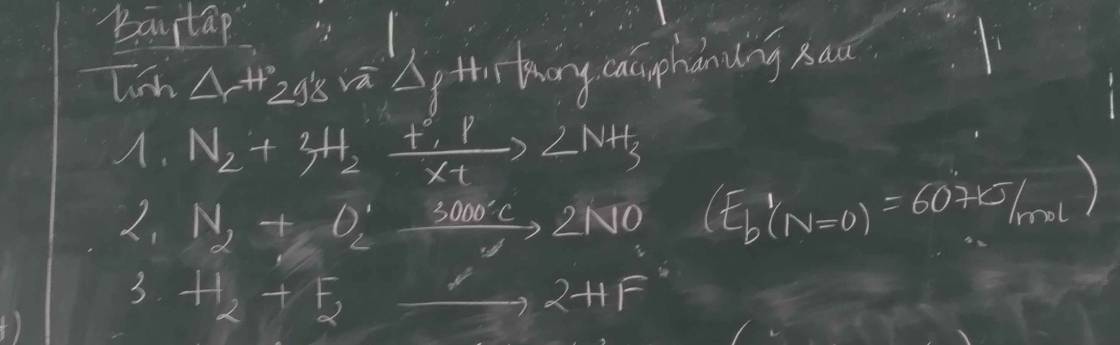a: \(\left\{{}\begin{matrix}2x-y-z=2\\x+y=3\\x-y+2z=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y-z=2\\2x+2y=6\\2x-2y+4z=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3y-z=-4\\y-5z=-2\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{9}{8}\\z=\dfrac{5}{8}\\x=3-\dfrac{9}{8}=\dfrac{15}{8}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}3x+y-z=2\\x+2y+z=5\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+y-z=2\\3x+6y+3z=15\\3x+3y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-5y-4z=-13\\-2y-z=-4\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\z=2\\x=1\end{matrix}\right.\)