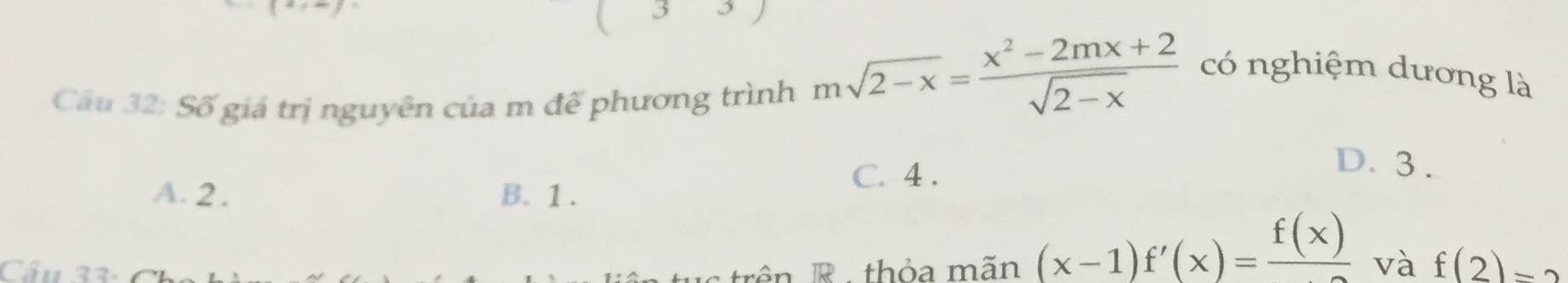ĐKXĐ: \(x< 2\)
\(m\sqrt{2-x}=\dfrac{x^2-2mx+2}{\sqrt{2-x}}\Rightarrow m\left(2-x\right)=x^2-2mx+2\)
\(\Leftrightarrow x^2+2=m\left(x+2\right)\Rightarrow m=\dfrac{x^2+2}{x+2}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2}{x+2}\) với \(0< x< 2\)
\(f'\left(x\right)=\dfrac{2x\left(x+2\right)-\left(x^2+2\right)}{\left(x+2\right)^2}=\dfrac{x^2+4x-2}{\left(x+2\right)^2}=0\Rightarrow x=-2+\sqrt{6}\)
\(f\left(0\right)=1;f\left(2\right)=\dfrac{3}{2};f\left(-2+\sqrt{6}\right)=-4+2\sqrt{6}\)
\(\Rightarrow-4+2\sqrt{6}\le m< \dfrac{3}{2}\)
\(\Rightarrow m=1\)
Có đúng 1 giá trị nguyên m thỏa mãn