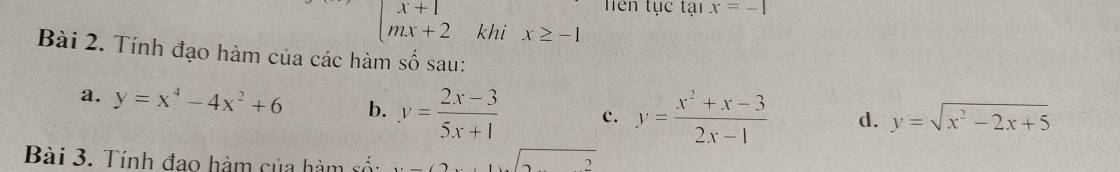3:
\(=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x^5}-1+\sqrt{2x+7}-3}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\dfrac{x^5-1}{\sqrt[3]{x^{10}}+\sqrt[3]{x^5}+1}+\dfrac{2x+7-9}{\sqrt{2x+7}+3}\right)\cdot\dfrac{1}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\dfrac{\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)}{\sqrt[3]{x^{10}}+\sqrt[3]{x^5}+1}+\dfrac{2\left(x-1\right)}{\sqrt{2x+7}+3}\right)\cdot\dfrac{1}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{x^4+x^3+x^2+x+1}{\sqrt[3]{x^{10}}+\sqrt[3]{x^5}+1}+\dfrac{2}{\sqrt{2x+7}+3}\)
\(=\dfrac{1+1+1+1+1}{1+1+1}+\dfrac{2}{3+3}=\dfrac{5}{3}+\dfrac{1}{3}=2\)
Đúng 0
Bình luận (0)
