a.
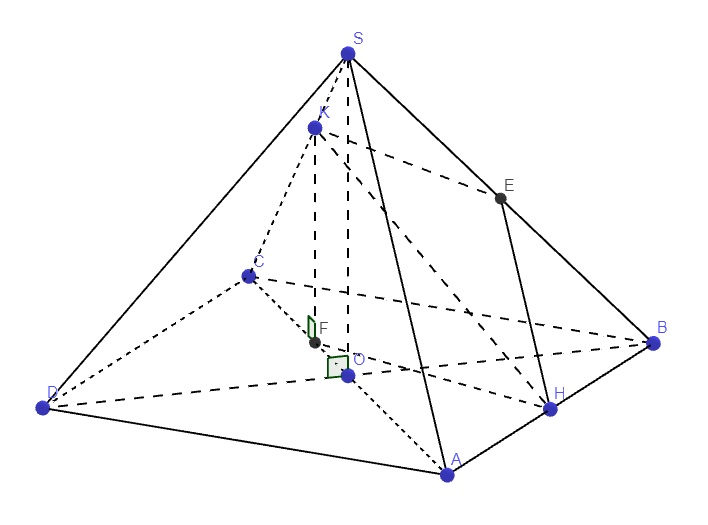
\(O=AC\cap BD\Rightarrow O\in BD\in\left(SBD\right)\) \(\Rightarrow SO\in\left(SBD\right)\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\Rightarrow AC\perp SD\)
b.
O là trung điểm AC, H là trung điểm AB \(\Rightarrow\) OH là đường trung bình tam giác ABC
\(\Rightarrow OH||BC\Rightarrow OH\perp AB\Rightarrow OH\perp CD\) (1)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SHO\right)\)
c.
Theo cmt trên \(OH||BC\Rightarrow OH||AD\)
\(\Rightarrow\widehat{\left(OH;SD\right)}=\widehat{\left(AD;SD\right)}=\widehat{SDA}\)
\(AC=2a\sqrt{2}\Rightarrow OA=a\sqrt{2}\Rightarrow SA=SB=SC=SD=\sqrt{SO^2+OA^2}=a\sqrt{3}\)
Áp dụng định lý hàm cosin trong tam giác SAD:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SDA}=...\)
d.
Gọi E là trung điểm SB \(\Rightarrow HE\) là đường trung bình tam giác SAB
\(\Rightarrow HE||SA\Rightarrow\widehat{\left(HK;SA\right)}=\widehat{\left(HK;HE\right)}=\widehat{KHE}\)
\(SK=\dfrac{1}{3}SC=\dfrac{a\sqrt{3}}{3}\) ; \(SE=\dfrac{1}{2}SB=\dfrac{a\sqrt{3}}{2}\) ; \(EH=\dfrac{1}{2}SA=\dfrac{a\sqrt{3}}{2}\)
\(cos\widehat{BSC}=\dfrac{SB^2+SC^2-BC^2}{2SB.SC}=\dfrac{1}{3}\)
\(\Rightarrow EK=\sqrt{SE^2+SK^2-2SE.SK.cos\widehat{BSC}}=\dfrac{a\sqrt{3}}{2}\)
Từ K kẻ KF song song SO \(\Rightarrow KF\perp\left(ABCD\right)\Rightarrow KF\perp HF\)
\(\dfrac{KF}{SO}=\dfrac{CK}{CS}=\dfrac{2}{3}\Rightarrow KF=\dfrac{2a}{3}\)
\(\dfrac{OF}{OC}=\dfrac{SK}{SC}=\dfrac{1}{3}\Rightarrow OF=\dfrac{1}{3}OC\Rightarrow AF=\dfrac{4}{3}OC=\dfrac{2}{3}AC=\dfrac{4a\sqrt{2}}{3}\)
\(\Rightarrow HF=\sqrt{AH^2+AF^2-2AH.AF.cos45^0}=\dfrac{a\sqrt{17}}{3}\)
\(\Rightarrow HK=\sqrt{HF^2+KF^2}=\dfrac{a\sqrt{21}}{3}\)
\(\Rightarrow cos\widehat{KHE}=\dfrac{HK^2+EH^2-EK^2}{2HK.EH}=\dfrac{\sqrt{7}}{3}\)