44.
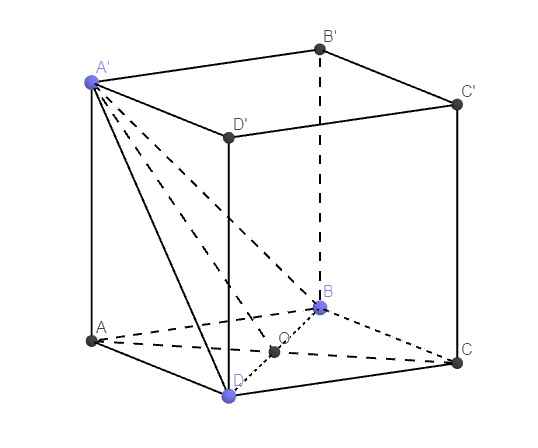
\(AB=\dfrac{BD}{\sqrt{2}}=2a\sqrt{2}\)
Gọi O là giao điểm AC và BD \(\Rightarrow AO\perp BD\Rightarrow BD\perp\left(A'AO\right)\)
\(\Rightarrow\widehat{A'OA}\) là góc giữa (A'BD) và (ABCD)
\(\Rightarrow\widehat{A'OA}=60^0\)
\(\Rightarrow A'A=AO.tan60^0=\dfrac{BD}{2}.tan60^0=2a\sqrt{3}\)
\(\Rightarrow V=A'A.AB^2=16\sqrt{3}a^3\)
45.
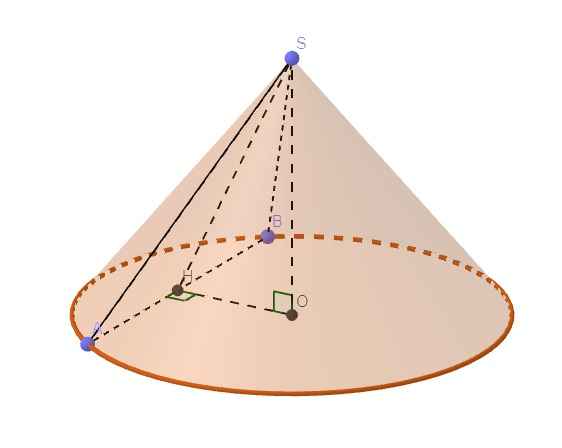
Đặt tên điểm như hình vẽ (với thiết diện của mặt phẳng và nón là tam giác SAB)
\(\Rightarrow\Delta SAB\) đều \(\Rightarrow SA=AB=2a\) ; \(SH=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\)
H là trung điểm AB \(\Rightarrow\widehat{SHO}=30^0\)
\(\Rightarrow OH=SH.cos30^0=\dfrac{3a}{2}\)
\(\Rightarrow R=OA=\sqrt{\left(\dfrac{AB}{2}\right)^2+OH^2}=\dfrac{a\sqrt{13}}{2}\)
\(\Rightarrow S_{xq}=\pi.R.SA=\sqrt{13}\pi a^2\)