a) Ta có: \(P\left(x\right)=7x^3+3x^4-x^2+5x^2-6x^3-2x^4+2017-x^3\)
\(=x^4+4x^2+2017\)
b) Bậc của P(x) là 4
c) Các hệ số của P(x) là 1;4;2017
Hệ số cao nhất là 4
Hệ số tự do là 2017
d) \(P\left(0\right)=0^4+4\cdot0^2+2017=2017\)
\(P\left(1\right)=1^4+4\cdot1^2+2017=1+4+2017=2022\)
\(P\left(-1\right)=\left(-1\right)^4+4\cdot\left(-1\right)^2+2017=1+4+2017=2022\)
e) \(P\left(-a\right)=\left(-a\right)^4+4\cdot\left(-a\right)^2+2017=a^4+4a^2+2017\)
\(P\left(a\right)=a^4+4a^2+2017\)
Do đó: P(-a)=P(a)








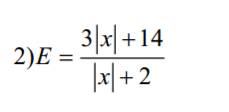 tìm gtln. tối nay mik phải nộp r, pls
tìm gtln. tối nay mik phải nộp r, pls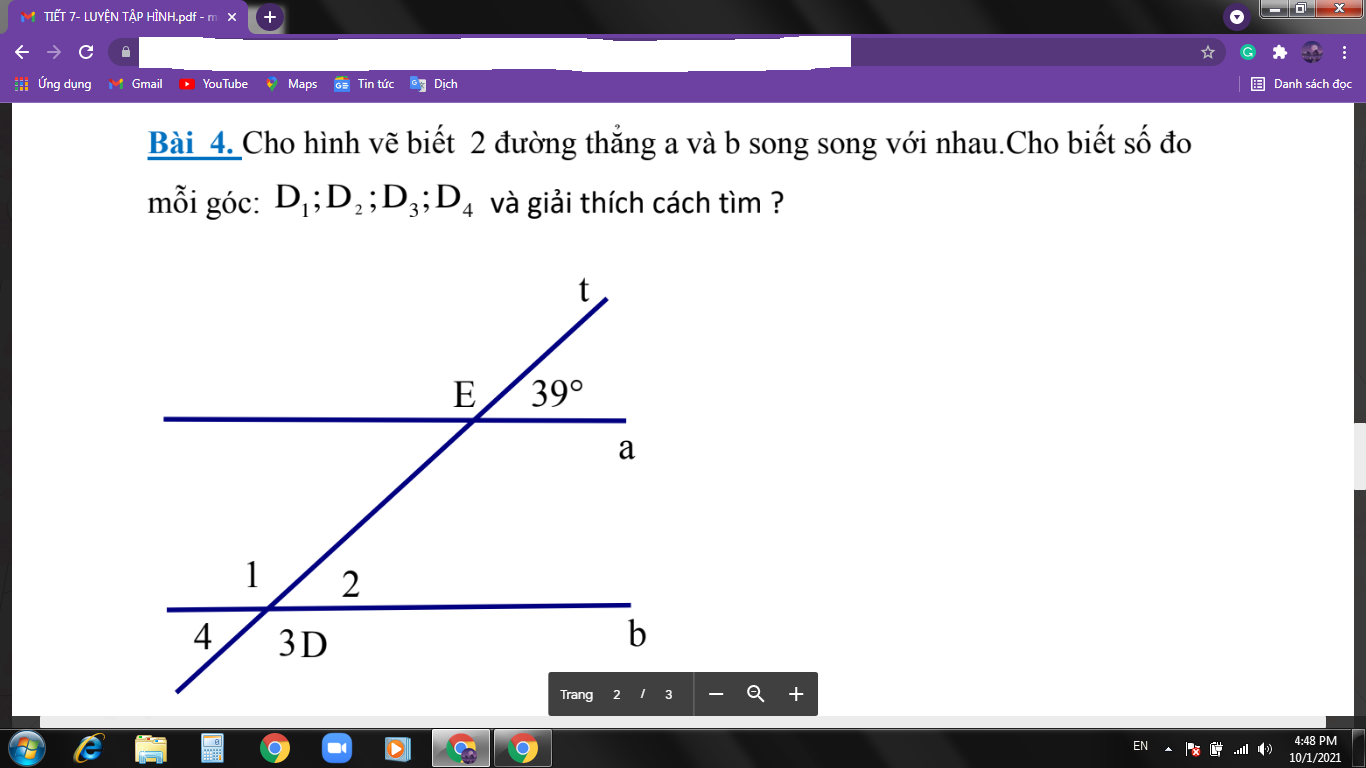 giúp mik với tối nay phải nộp rồi
giúp mik với tối nay phải nộp rồi



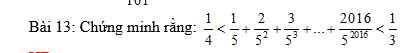 Giúp mik với ạ, chiều nay mik pk nộp r =((
Giúp mik với ạ, chiều nay mik pk nộp r =((


