a: Thay m=2 vào (d), ta được:
\(y=2\cdot\left(2-1\right)x-2^2+2\cdot2\)
\(=2x-4+4=2x\)
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=2x\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(x-2\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(0;0\right);\left(2;4\right)\right\}\)
b: Phương trình hoành độ giao điểm là:
\(x^2-2\left(m-1\right)x+m^2-2m=0\)
\(\Delta=\left(2m-2\right)^2-4\left(m^2-2m\right)\)
\(=4m^2-8m+4-4m^2+8m=4\)
Do đó: Phương trình luôn có hai nghiệm phân biệt
Theo đề, ta có: \(2\left(m-1\right)=0\)
hay m=1


 giúp mik câu b) vs ạ :,>
giúp mik câu b) vs ạ :,>








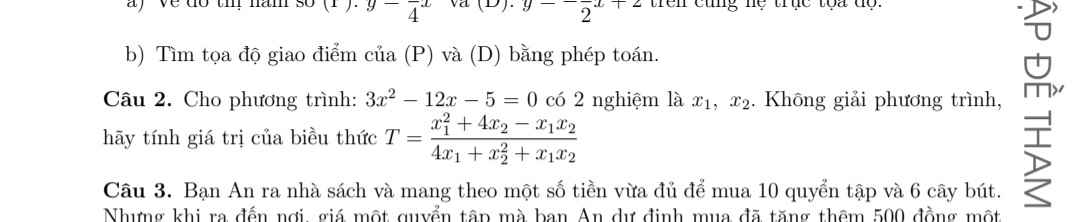

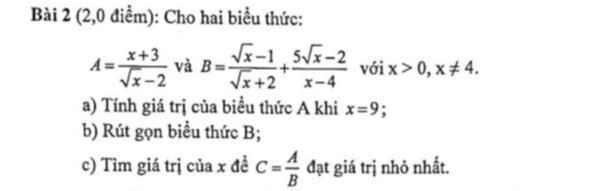 mn giúp mik câu c vs ạ
mn giúp mik câu c vs ạ
 giúp câu c vs ạ,mik cần gấp
giúp câu c vs ạ,mik cần gấp mọi người giúp mik bài 4 câu a vs ạ
mọi người giúp mik bài 4 câu a vs ạ 