a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔAMB=ΔAMC
b: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: AH=AK và MH=MK
=>AM là đường trung trực của HK
tui làm hộ bài 5 cho, cần ko lười làm mấy bài hình lém :D?
\(\text{a)Xét }\Delta AMB\text{ và }\Delta AMC\text{ có:}\)
\(\left\{{}\begin{matrix}AM\text{ chung}\\\widehat{BAM}=\widehat{CAM}\left(AM\text{ là phân giác }\widehat{BAC}\right)\\AB=AC\left(\Delta ABC\text{ cân tại A}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c-g-c\right)\)
\(\text{b)Xét }\Delta AHM\text{ và }\Delta AKM\text{ có:}\)
\(\left\{{}\begin{matrix}AM\text{ chung}\\\widehat{AHM}=\widehat{AKM}=90^0\left(gt\right)\\\widehat{HAM}=\widehat{KAM}\left(AM\text{ là phân giác }\widehat{BAC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHM=\Delta AKM\left(g-c-g\right)\)
\(\Rightarrow AH=AK\left(\text{hai cạnh tương ứng}\right)\)
\(\text{c)K bt;-;}\)

























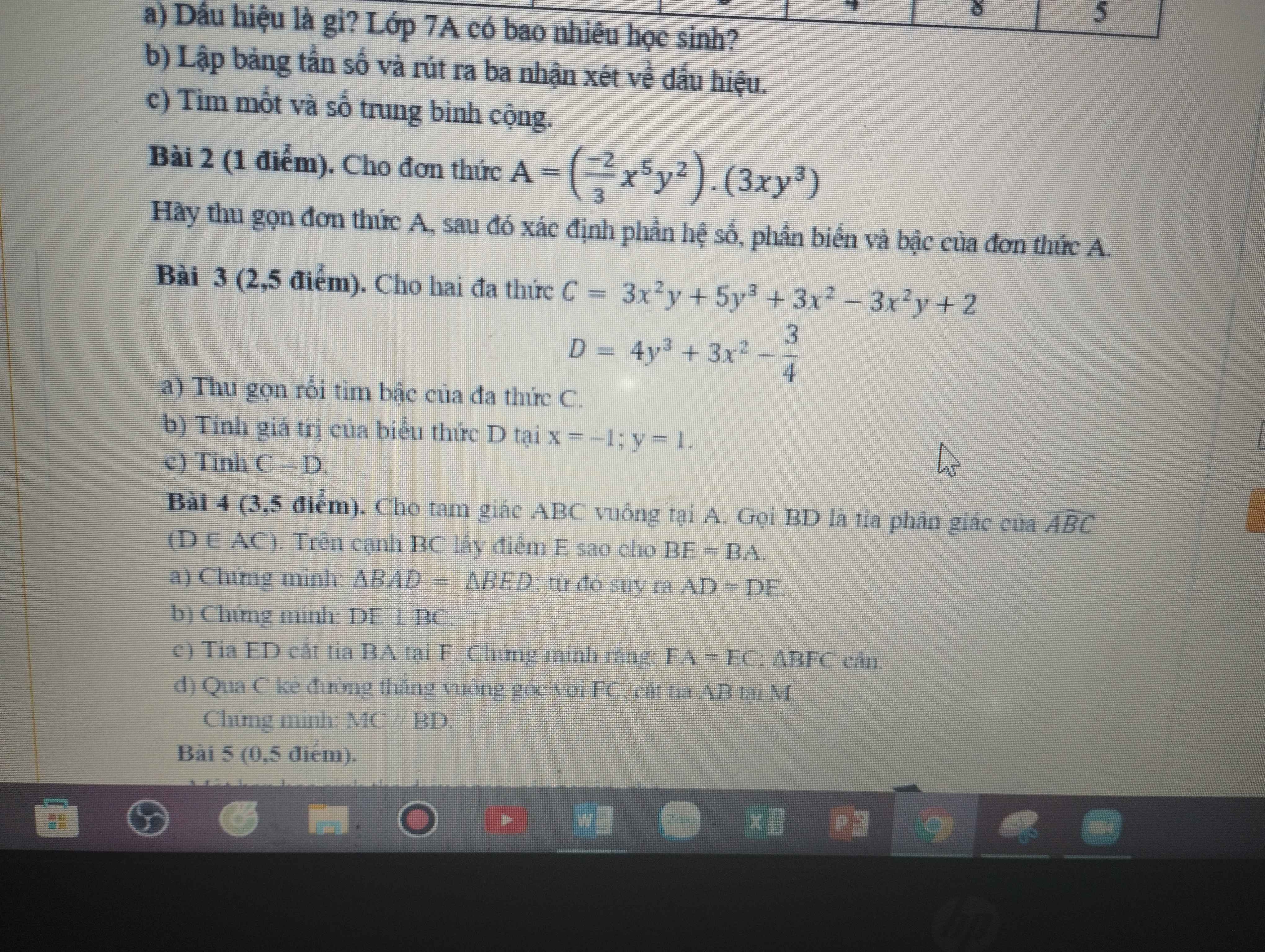
 giúp mik câu c bài 3 và hết bài 4 vs ạ
giúp mik câu c bài 3 và hết bài 4 vs ạ