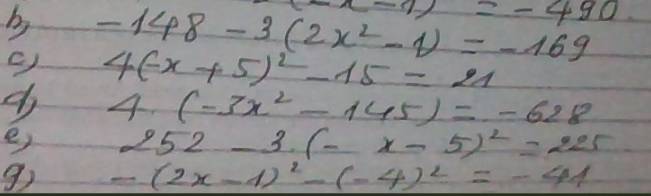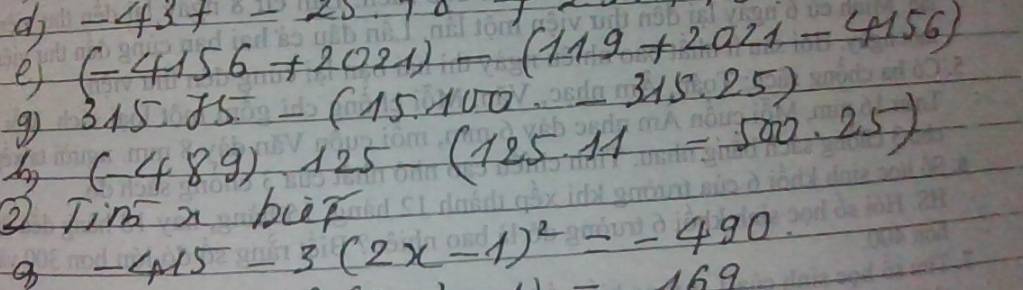Lời giải:
b. $-138-3(2x^2-1)=-169$
$3(2x^2-1)=-148-(-169)=21$
$2x^2-1=21:3=7$
$2x^2=7+1=8$
$x^2=4=2^2=(-2)^2\Rightarrow x=\pm 2$
c.
$4(-x+5)^2-15=21$
$4(-x+5)^2=21+15=36$
$(-x+5)^2=36:4=9=3^2=(-3)^2$
$\Rightarrow -x+5=3$ hoặc $-x+5=-3$
$\Rightarrow x=2$ hoặc $x=8$
d.
$4(-3x^2-145)=-628$
$-3x^2-145=-628:4=-157$
$3x^2+145=157$
$3x^2=157-145=12$
$x^2=12:3=4=2^2=(-2)^2$
$\Rightarrow x=\pm 2$
e.
$252-3(-x-5)^2=225$
$3(-x-5)^2=252-225=27$
$(-x-5)^2=27:3=9$
$(x+5)^2=3^2=(-3)^2$
$\Rightarrow x+5=3$ hoặc $x+5=-3$
$\Rightarrow x=-2$ hoặc $x=-8$
g.
$-(2x-1)^2-(-4)^2=-41$
$(2x-1)^2+(-4)^2=41$
$(2x-1)^2+16=41$
$(2x-1)^2=41-16=25=5^2=(-5)^2$
$\Rightarrow 2x-1=5$ hoặc $2x-1=-5$
$\Rightarrow x=3$ hoặc $x=-2$
b: \(-148-3\left(2x^2-1\right)=-169\)
=>\(148+3\left(2x^2-1\right)=169\)
=>\(3\left(2x^2-1\right)=21\)
=>\(2x^2-1=\dfrac{21}{3}=7\)
=>\(2x^2=1+7=8\)
=>x2=4
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
c: \(4\left(x+5\right)^2-15=21\)
=>\(4\left(x+5\right)^2=21+15=36\)
=>\(\left(x+5\right)^2=\dfrac{36}{4}=9\)
=>\(\left[{}\begin{matrix}x+5=3\\x+5=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-8\end{matrix}\right.\)
d: \(4\left(-3x^2-145\right)=-628\)
=>\(-4\left(3x^2+145\right)=-628\)
=>\(3x^2+145=\dfrac{-628}{-4}=157\)
=>\(3x^2=157-145=12\)
=>x2=4
=>\(\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
e: \(252-3\left(-x-5\right)^2=225\)
=>\(252-3\left(x+5\right)^2=225\)
=>\(3\left(x+5\right)^2=252-225=27\)
=>\(\left(x+5\right)^2=9\)
=>\(\left[{}\begin{matrix}x+5=3\\x+5=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-8\end{matrix}\right.\)
g: \(-\left(2x-1\right)^2-\left(-4\right)^2=-41\)
=>\(\left(2x-1\right)^2+16=41\)
=>\(\left(2x-1\right)^2=25\)
=>\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)