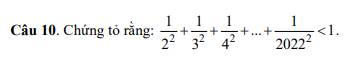z4:
\(\dfrac{24}{148}=\dfrac{6}{37}=\dfrac{108}{37\cdot18}\)
\(\dfrac{-14}{-36}=\dfrac{7}{18}=\dfrac{7\cdot37}{18\cdot37}=\dfrac{259}{37\cdot18}\)
mà 108<259
nên \(\dfrac{24}{148}< \dfrac{-14}{-36}\)
z5: \(\dfrac{-26}{-72}=\dfrac{26}{72}< 1\)
\(1< \dfrac{45}{20}=\dfrac{-45}{-20}\)
Do đó: \(\dfrac{-26}{-72}< \dfrac{-45}{-20}\)
z6: \(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{1\cdot4}{3\cdot4}=\dfrac{4}{12}\)
\(\dfrac{21}{28}=\dfrac{3}{4}=\dfrac{3\cdot3}{4\cdot3}=\dfrac{9}{12}\)
mà 4<9
nên \(\dfrac{14}{42}< \dfrac{21}{28}\)
z7: \(\dfrac{-14}{-56}=\dfrac{1}{4}=\dfrac{5}{20}\)
\(\dfrac{21}{35}=\dfrac{3}{5}=\dfrac{3\cdot4}{5\cdot4}=\dfrac{12}{20}\)
mà 5<12
nên \(\dfrac{-14}{-56}< \dfrac{21}{35}\)
z8: \(10A=\dfrac{10^{201}+10}{10^{201}+1}=1+\dfrac{9}{10^{201}+1}\)
\(10B=\dfrac{10^{202}+10}{10^{202}+1}=1+\dfrac{9}{10^{202}+1}\)
\(10^{201}+1< 10^{202}+1\)
=>\(\dfrac{9}{10^{201}+1}>\dfrac{9}{10^{202}+1}\)
=>\(\dfrac{9}{10^{201}+1}+1>\dfrac{9}{10^{202}+1}+1\)
=>10A>10B
=>A>B





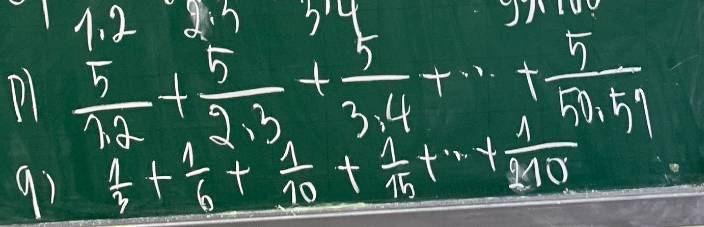

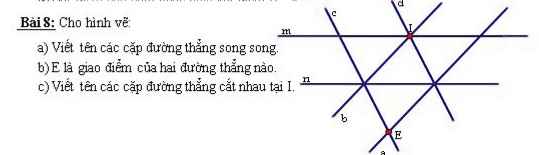




 Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.
Giúp em với ạ, em cần gấp trước 7h15 ạ. Em cảm ơn nhiều.