a) Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\widehat{AOB}< \widehat{AOC}\left(60^0< 120^0\right)\)
nên tia OB nằm giữa hai tia OA và OC
b) Ta có: tia OB nằm giữa hai tia OA và OC(cmt)
nên \(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)
hay \(\widehat{BOC}=60^0\)
c) Ta có: tia OB nằm giữa hai tia OA và OC(cmt)
mà \(\widehat{AOB}=\widehat{BOC}\left(=60^0\right)\)
nên OB là tia phân giác của \(\widehat{AOC}\)
d) Ta có: OM là tia phân giác của \(\widehat{BOC}\)
nên \(\widehat{COM}=\dfrac{\widehat{COB}}{2}=\dfrac{60^0}{2}=30^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{COM}< \widehat{COA}\left(30^0< 120^0\right)\)
nên tia OM nằm giữa hai tia OA và OC
\(\Leftrightarrow\widehat{COM}+\widehat{AOM}=\widehat{AOC}\)
hay \(\widehat{AOM}=90^0\)








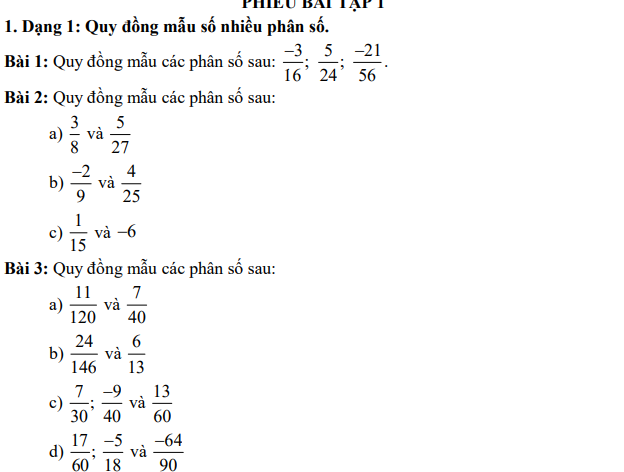









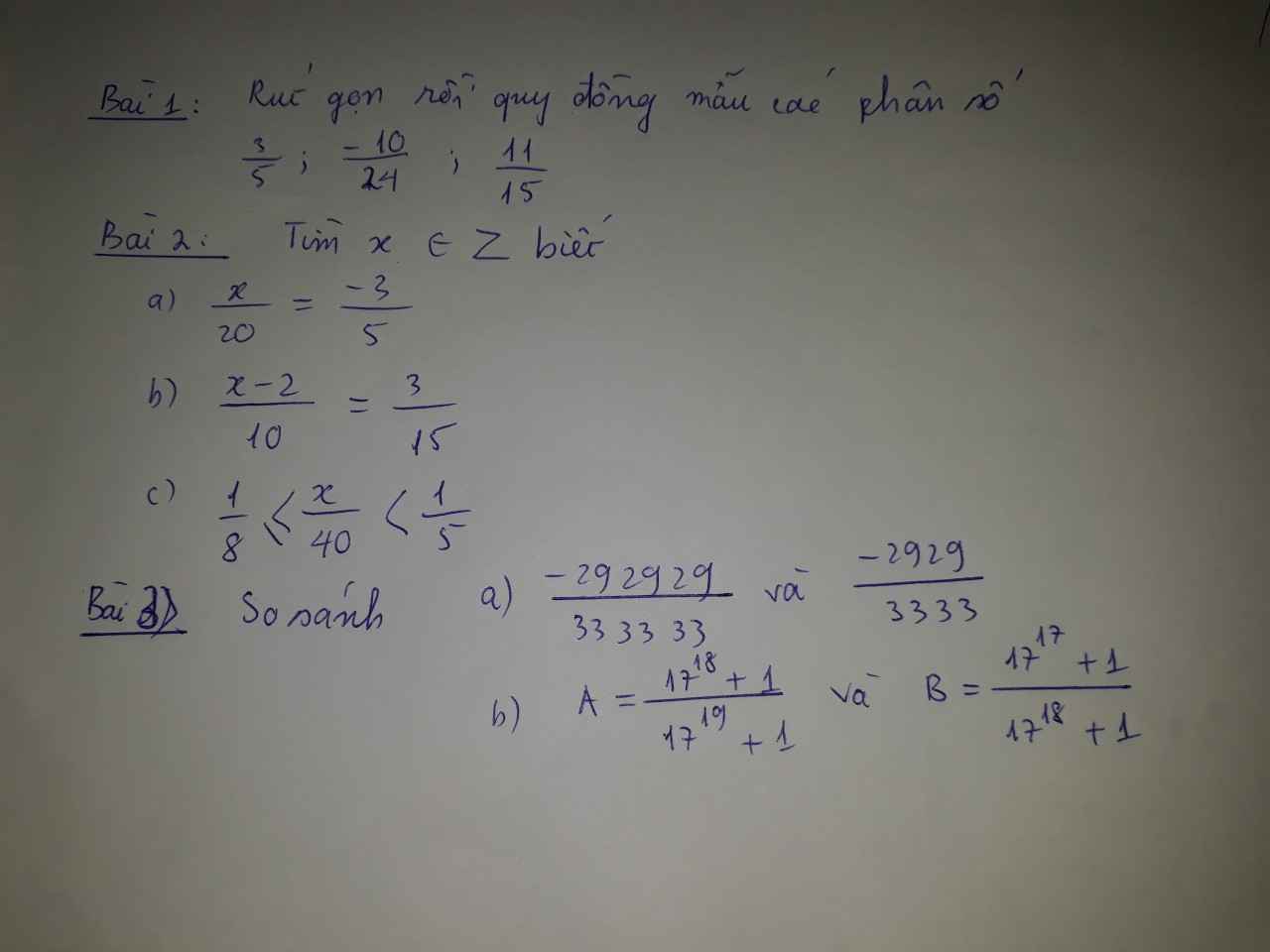


 Giúp em vs ạ
Giúp em vs ạ