`# \text {Ryo}`
`3,`
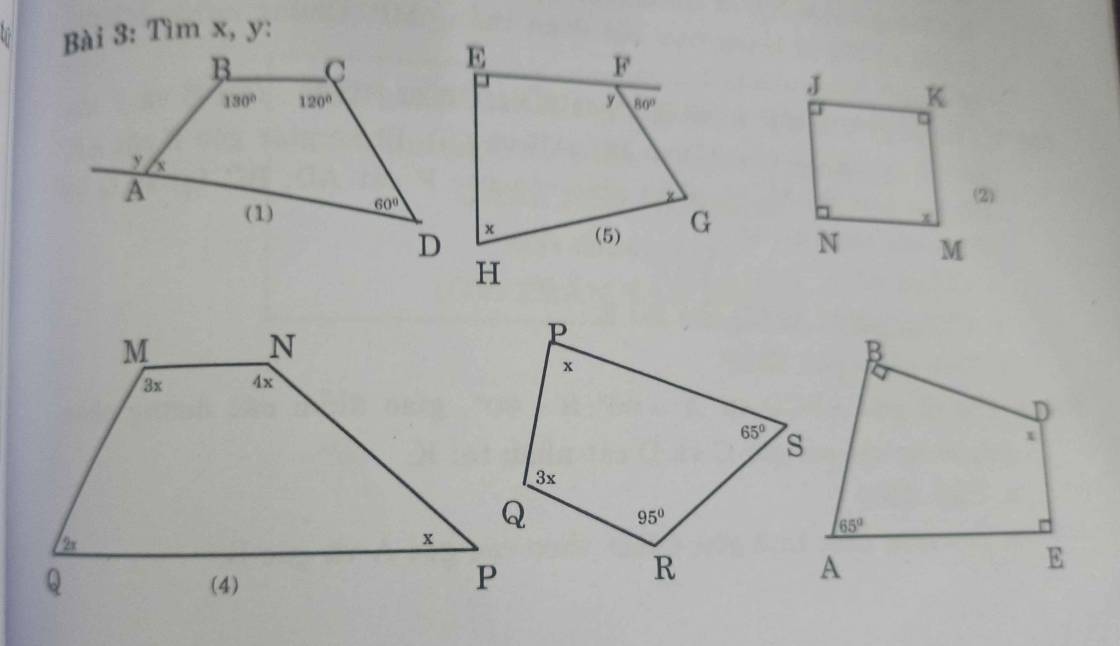
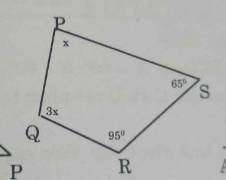
Xét tứ giác ABCD:
\(\widehat{\text{A}}+\widehat{\text{B}}+\widehat{\text{C}}+\widehat{\text{D}}=360^0\left(\text{định lý tổng các góc của tứ giác}\right)\\ \Rightarrow\widehat{x}+130^0+120^0+60^0=360^0\\ \Rightarrow\widehat{x}=50^0\)
Ta có:
`x + y = 180^0 (\text {kề bù})`
`=> 50^0 + y = 180^0`
`=> y = 130^0`
Vậy, `x = 50^0; y = 130^0`
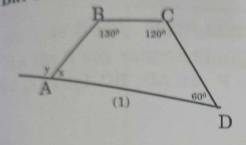
Xét tứ giác MNJK:
\(\widehat{\text{M}}+\widehat{\text{N}}+\widehat{\text{J}}+\widehat{\text{K}}=360^0\\\Rightarrow \widehat{x}+90^0+90^0+90^0=360^0\\ \Rightarrow\widehat{x}=90^0\)
Vậy, `x = 90^0`
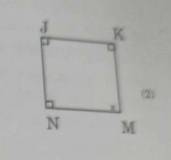
Xét tứ giác PQRS:
\(\widehat{\text{P}}+\widehat{\text{Q}}+\widehat{\text{R}}+\widehat{\text{S}}=360^0\\ \Rightarrow\widehat{\text{P}}+\widehat{\text{Q}}+95^0+65^0=360^0\\ \Rightarrow\widehat{\text{P}}+\widehat{\text{Q}}=200^0\)
Ta có:
\(\widehat{\text{P}}+\widehat{\text{Q}}=200^0\\ \Rightarrow x+3x=200^0\\ \Rightarrow4x=200^0\\ \Rightarrow x=50^0\)
Vì \(\widehat{\text{Q}}\) `= 3*x`
`=>`\(\widehat{\text{Q}}=3\cdot50^0=150^0\)
Vậy, `x = 50^0; 3x = 150^0`
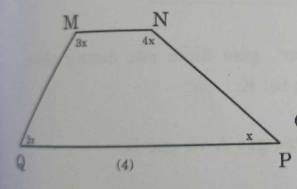
Xét tứ giác MNPQ:
\(\widehat{\text{M}}+\widehat{\text{N}}+\widehat{\text{P}}+\widehat{\text{Q}}=360^0\\ \Rightarrow3x+4x+x+2x=360^0\\ \Rightarrow\left(3+4+1+2\right)x=360^0\\ \Rightarrow 10x=360^0\\ \Rightarrow x=36^0\)
Ta có:
\(\widehat{\text{M}}=3\cdot x\\ \widehat{\text{N}}=4\cdot x\\ \widehat{\text{Q}}=2\cdot x\)
\(\Rightarrow\widehat{\text{M}}=3\cdot36=108^0\\ \widehat{\text{N}}=4\cdot36=144^0\\ \widehat{\text{Q}}=2\cdot36=72^0\)
Vậy, `x = 36^0; 2x = 72^0; 3x = 108^0; 4x = 144^0.`
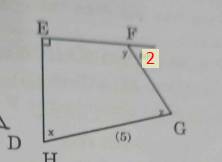
Ta có:
\(\widehat{\text{F}_2}+\widehat{\text{ EFG}}=180^0\left(\text{kề bù}\right)\\ \Rightarrow80^0+y=180^0\\ \Rightarrow y=100^0\)
Xét tứ giác EFGH:
\(\widehat{\text{E}}+\widehat{\text{F}}+\widehat{\text{G}}+\widehat{\text{H}}=360^0\\ \Rightarrow90^0+100^0+\text{ }\widehat{\text{G}}+\widehat{\text{H}}=360^0\\ \Rightarrow\widehat{\text{G}}+\widehat{\text{H}}=170^0\)
Ta có:
\(\widehat{\text{G}}+\widehat{\text{H}}=170^0\\ \Rightarrow x+x=170^0\\ \Rightarrow 2x=170^0\\ \Rightarrow x=85^0\)
Vậy, `x = 85^0; y = 100^0.`
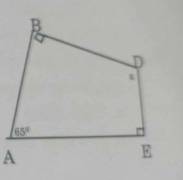
Xét tứ giác ABDE:
\(\widehat{\text{A}}+\widehat{\text{B}}+\widehat{\text{D}}+\widehat{\text{E}}=360^0\\ \Rightarrow65^0+90^0+x+90^0=360^0\\ \Rightarrow x=115^0\)
Vậy, `x = 115^0.`
(1) \(x=360^o-60^o-130^o-120^o=50^o\)
\(y=180^o-50^o=130^o\)
(2) \(x=360^o-3\cdot90^o=90^o\)
(3) \(\widehat{Q}+\widehat{R}+\widehat{S}=65^o+95^o+3x=160^o+3x\)
\(x=360^o-160^o-3x\Leftrightarrow4x=200^o\Leftrightarrow x=50^o\)
(4) \(\widehat{M}+\widehat{N}+\widehat{Q}+\widehat{P}=360^o\)
\(\Rightarrow3x+4x+2x+x=360^o\)
\(\Leftrightarrow10x=360^o\)
\(\Leftrightarrow x=36^o\)
(5) \(y=180^o-80^o=100^o\)
\(\Rightarrow x+x=360^o-90^o-100^o\)
\(\Leftrightarrow2x=170^o\)
\(\Leftrightarrow x=85^o\)
(6) \(x=360^o-2\cdot90^o-65^o=115^o\)
(1) \(x=360-\left(120+130+60\right)=50^o\)
\(y=180-50=130^o\)
(4) \(x+2x+3x+4x=360\)
\(\Rightarrow10x=360\)
\(\Rightarrow x=36^o\)
(2) \(x=90^o\)
(5) \(y=180-80=100^o\)
\(2x+90+100=360\)
\(\Rightarrow2x=170\)
\(\Rightarrow x=85^o\)
(6) \(4x+95+65=360\)
\(\Rightarrow4x=200\)
\(\Rightarrow x=50^o\)
(3) \(x+90+90+65=360\)
\(\Rightarrow x=115\)