Bài 24:
a: Để A có nghĩa thì \(\left\{{}\begin{matrix}x-2>=0\\\sqrt{x-2}-1< >0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=2\\x\ne3\end{matrix}\right.\)
b: \(A^2=\dfrac{x-1-2\sqrt{x-2}}{\left(\sqrt{x-2}-1\right)^2}=\dfrac{x-2-2\sqrt{x-2}+1}{\left(\sqrt{x-2}-1\right)^2}\)
\(=\dfrac{\left(\sqrt{x-2}-1\right)^2}{\left(\sqrt{x-2}-1\right)^2}=1\)
=>\(A=\pm1\)
Bài 26:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x-4>=0\\1-\dfrac{8}{x}+\dfrac{16}{x^2}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=4\\\left(1-\dfrac{4}{x}\right)^2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=4\\1-\dfrac{4}{x}\ne0\end{matrix}\right.\)
=>x>4
b: \(B=\dfrac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\dfrac{8}{x}+\dfrac{16}{x^2}}}\)
\(=\dfrac{\sqrt{x-4+2\cdot\sqrt{x-4}\cdot2+4}+\sqrt{x-4-2\cdot\sqrt{x-4}\cdot2+4}}{\sqrt{\left(1-\dfrac{4}{x}\right)^2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{x-4}+2\right)^2}+\sqrt{\left(\sqrt{x-4}-2\right)^2}}{\left|1-\dfrac{4}{x}\right|}\)
\(=\dfrac{\sqrt{x-4}+2+\left|\sqrt{x-4}-2\right|}{1-\dfrac{4}{x}}\)
TH1: \(\sqrt{x-4}-2>=0\)
=>x-4>=4
=>x>=8
\(B=\dfrac{\sqrt{x-4}+2+\sqrt{x-4}-2}{1-\dfrac{4}{x}}\)
\(=2\sqrt{x-4}:\dfrac{x-4}{x}=\dfrac{2x}{\sqrt{x-4}}\)
TH2: 4<x<8
\(B=\dfrac{\sqrt{x-4}+2-\sqrt{x-4}+2}{1-\dfrac{4}{x}}=4:\dfrac{x-4}{x}=\dfrac{4x}{x-4}\)
c: TH1: x>=8
Để B nguyên thì \(2x⋮\sqrt{x-4}\)
=>\(2x-8+8⋮\sqrt{x-4}\)
=>\(8⋮\sqrt{x-4}\)
=>\(\sqrt{x-4}\in\left\{1;2;4;8\right\}\)
=>\(x-4\in\left\{1;4;16;64\right\}\)
=>\(x\in\left\{5;8;20;68\right\}\)
mà x>=8
nên \(x\in\left\{8;20;68\right\}\)
TH2: 4<x<8
Để B nguyên thì \(4x⋮x-4\)
=>\(4x-16+16⋮x-4\)
=>\(16⋮x-4\)
mà x-4>0
nên \(x-4\in\left\{1;2;4;8;16\right\}\)
=>\(x\in\left\{5;6;8;12;20\right\}\)
mà x<8
nên \(x\in\left\{5;6\right\}\)
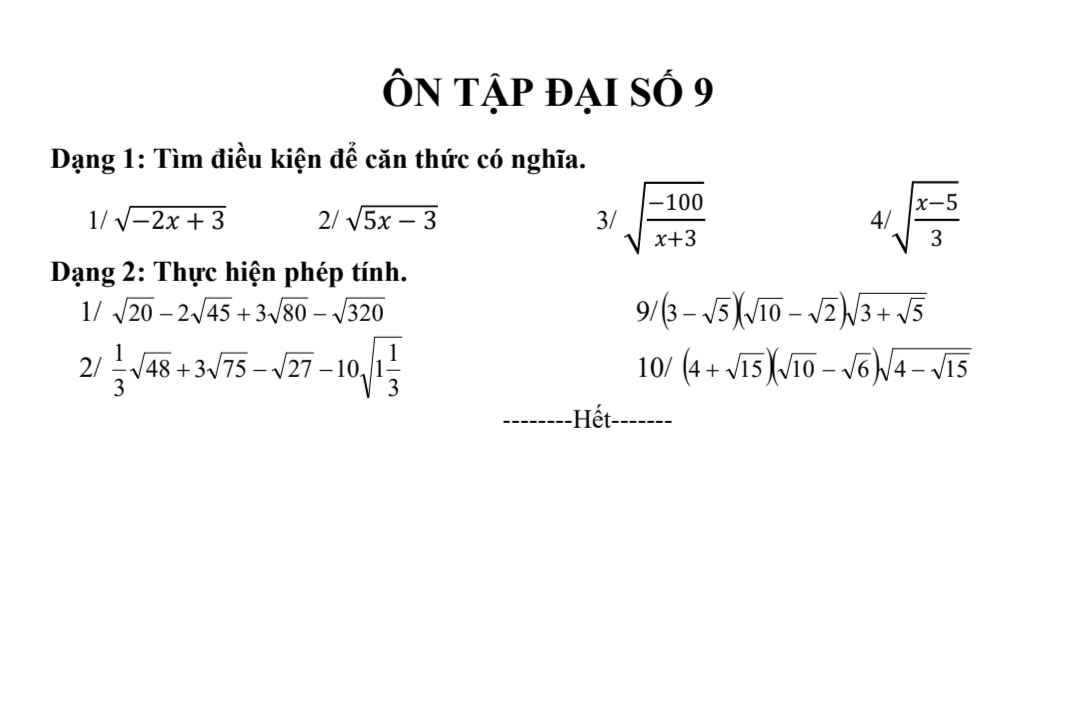
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
