a. \(\sqrt{9x^2}-2x\)
= \(\sqrt{\left(3x\right)^2}-2x\)
= 3x - 2x
= x(3 - 2)
= x
b. \(2\sqrt{x^2}\)
= 2 . x
= 2x
c. \(3\sqrt{\left(x-2\right)^2}\)
= 3(x - 2)
= 3x - 6
d. \(2\sqrt{x^2}-5x\)
= 2x - 5x
= x(2 - 5)
= -3x
\(a,=\left|3x\right|-2x=-3x-2x=-5x\\ b,=2\left|x\right|=2x\\ c,=3\left|x-2\right|=3\left(2-x\right)=6-3x\\ d,=2\left|x\right|-5x=-2x-5x=-7x\)
a) \(\sqrt{9x^2}-2x\left(x< 0\right)\\ =\left|3x\right|-2x\\ =3x-2x\left(\text{vì }-3x>0\right)\\ =x\)
b) \(2\sqrt{x^2}\left(x\ge0\right)\\ =2\left|x\right|\\ =2x\left(\text{vì }x\ge0\right)\)
c) \(3\sqrt{\left(x-2\right)^2}\left(x< 2\right)\\ =3\left|x-2\right|\\ =3\left(2-x\right)\left(\text{vì }x-2< 0\right)\\ =6-3x\)
d) \(2\sqrt{x^2}-5x\left(x< 0\right)\\ =2\left|x\right|-5x\\ =-2x-5x\left(\text{vì }x< 0\right)\\ =-7x\)
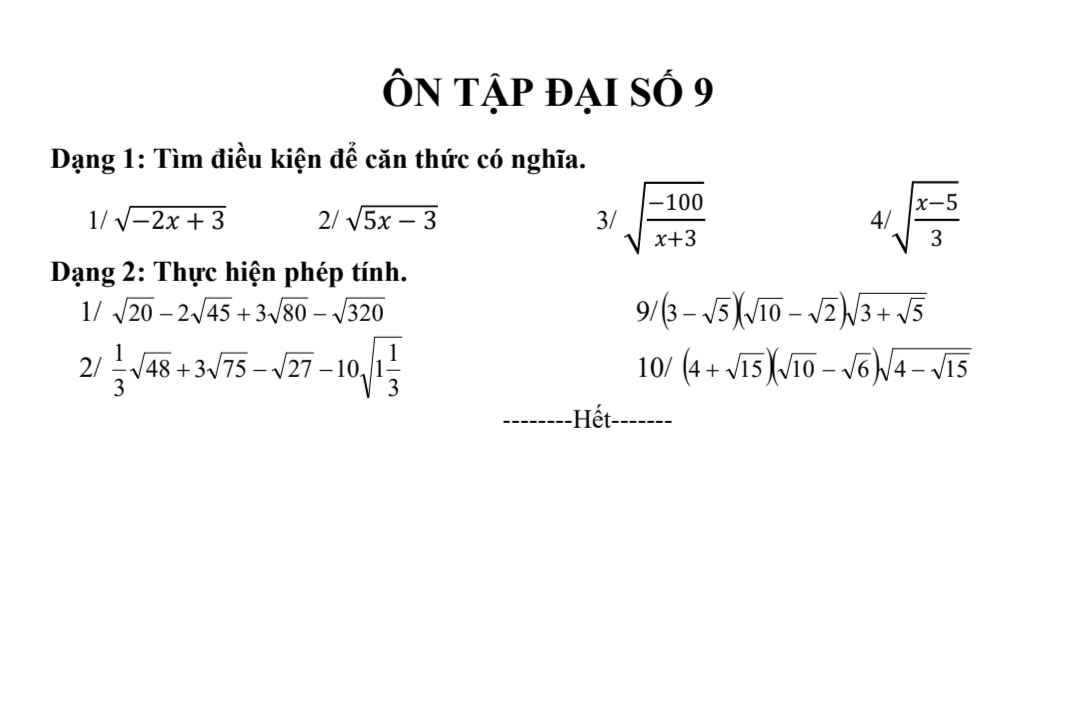
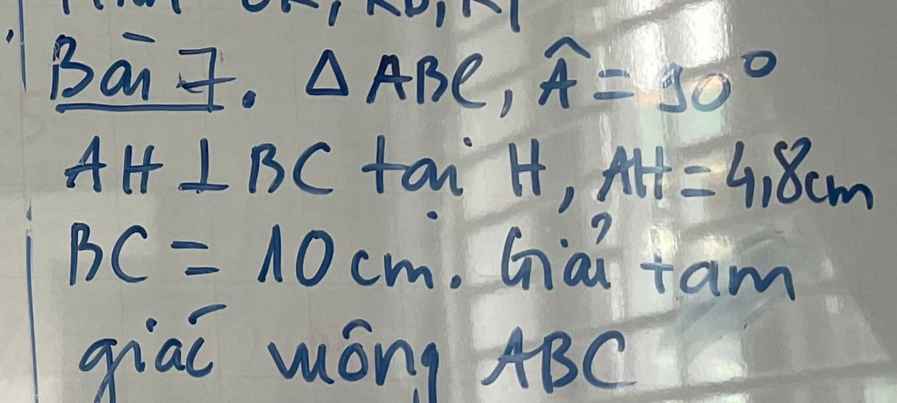
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
