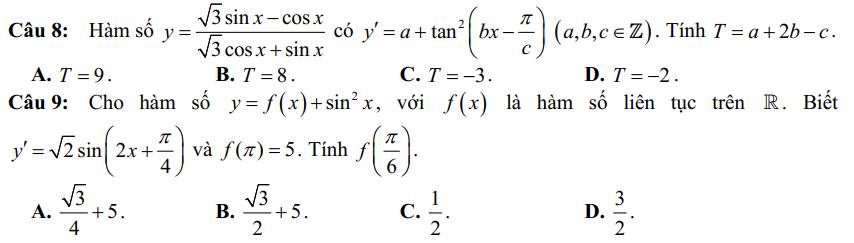Câu 23:
ĐKXĐ: \(-5x^2+14x-9>=0\)
=>\(5x^2-14x+9< =0\)
=>(x-1)(5x-9)<=0
=>\(1< =x< =\dfrac{9}{5}\)
\(f'\left(x\right)=\left(\sqrt{-5x^2+14x-9}\right)'\)
\(=\dfrac{\left(-5x^2+14x-9\right)'}{2\sqrt{-5x^2+14x-9}}\)
\(=\dfrac{-10x+14}{2\sqrt{-5x^2+14x-9}}=\dfrac{-5x+7}{\sqrt{-5x^2+14x-9}}\)
f'(x)<0
=>-5x+7<0
=>x>7/5
mà 1<=x<=9/5
nên \(\dfrac{7}{5}< x< =\dfrac{9}{5}\)
=>a=7/5;b=9/5
\(3a+b=\dfrac{21}{5}+\dfrac{9}{5}=6\)
=>Chọn C
Câu 8:
\(y=\dfrac{\sqrt{3}\cdot sinx-cosx}{\sqrt{3}\cdot cosx+sinx}\)
\(=\dfrac{\dfrac{\sqrt{3}}{2}\cdot sinx-\dfrac{1}{2}\cdot cosx}{\dfrac{\sqrt{3}}{2}\cdot cosx+\dfrac{1}{2}\cdot sinx}\)
\(=\dfrac{sinx\cdot cos\left(\dfrac{\Omega}{6}\right)-cosx\cdot sin\left(\dfrac{\Omega}{6}\right)}{cosx\cdot sin\left(\dfrac{\Omega}{3}\right)+sinx\cdot cos\left(\dfrac{\Omega}{3}\right)}\)
\(=\dfrac{sin\left(x-\dfrac{\Omega}{6}\right)}{sin\left(x+\dfrac{\Omega}{3}\right)}=\dfrac{sin\left(x-\dfrac{\Omega}{6}\right)}{cos\left(\dfrac{\Omega}{2}-x-\dfrac{\Omega}{3}\right)}\)
\(=\dfrac{sin\left(x-\dfrac{\Omega}{6}\right)}{cos\left(x-\dfrac{\Omega}{6}\right)}=tan\left(x-\dfrac{\Omega}{6}\right)\)
=>\(y'=\left(x-\dfrac{\Omega}{6}\right)'\left(1+tan^2\left(x-\dfrac{\Omega}{6}\right)\right)\)
\(=1+tan^2\left(x-\dfrac{\Omega}{6}\right)\)
=>a=1; b=1; c=6
T=a+2b-c=1+2-6=-3
=>Chọn C
9.
\(y'=f'\left(x\right)+2sinx.cosx=f'\left(x\right)+sin2x\)
\(\Rightarrow f'\left(x\right)+sin2x=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Rightarrow f'\left(x\right)+sin2x=sin2x+cos2x\)
\(\Rightarrow f'\left(x\right)=cos2x\)
\(\Rightarrow f\left(x\right)=\int cos2xdx=\dfrac{1}{2}sin2x+C\)
\(f\left(\pi\right)=5\Rightarrow\dfrac{1}{2}sin\left(2\pi\right)+C=5\Rightarrow C=5\)
\(\Rightarrow f\left(x\right)=\dfrac{1}{2}sin2x+5\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}sin\left(\dfrac{\pi}{3}\right)+5=\dfrac{\sqrt{3}}{4}+5\)
24.
\(y'=\left(3x^2+2mx+3\right).3^{x^3+mx^2+3x+1}.ln3\)
\(y'\ge0\Leftrightarrow3x^2+2mx+3\ge0\) (do \(3^{x^3+mx^2+3x+1}.ln3\ge0;\forall x;m\))
\(\Rightarrow\Delta'=m^2-9\le0\)
\(\Rightarrow-3\le m\le3\)
Có 7 giá trị nguyên của m thỏa mãn