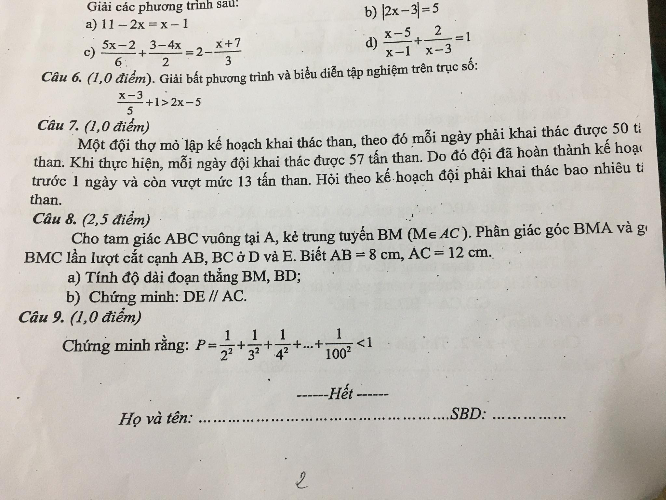Bài 8:
2: ĐKXĐ: \(x-1\ne0\)
=>\(x\ne0+1\)
=>\(x\ne1\)
11: ĐKXĐ: \(x^2-4\ne0\)
=>\(x^2\ne4\)
=>\(x\notin\left\{2;-2\right\}\)
13: ĐKXĐ: \(5x^2+x\ne0\)
=>\(x\left(5x+1\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne0\\5x+1\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne0\\x\ne-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(x\notin\left\{0;-\dfrac{1}{5}\right\}\)
15: ĐKXĐ: \(\left(x+1\right)\left(x+3\right)\ne0\)
=>\(\left\{{}\begin{matrix}x+1\ne0\\x+3\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne-1\\x\ne-3\end{matrix}\right.\)
21: \(\dfrac{2x+7}{x^2+x-2}\)
ĐKXĐ: \(x^2+x-2\ne0\)
=>\(\left(x+2\right)\left(x-1\right)\ne0\)
=>\(\left\{{}\begin{matrix}x+2\ne0\\x-1\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne-2\\x\ne1\end{matrix}\right.\)
Vậy: \(x\notin\left\{-2;1\right\}\)
Bài 8:
2: ĐKXĐ: \(x-1\ne0\)
=>\(x\ne0+1\)
=>\(x\ne1\)
11: ĐKXĐ: \(x^2-4\ne0\)
=>\(x^2\ne4\)
=>\(x\notin\left\{2;-2\right\}\)
13: ĐKXĐ: \(5x^2+x\ne0\)
=>\(x\left(5x+1\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne0\\5x+1\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne0\\x\ne-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(x\notin\left\{0;-\dfrac{1}{5}\right\}\)
15: ĐKXĐ: \(\left(x+1\right)\left(x+3\right)\ne0\)
=>\(\left\{{}\begin{matrix}x+1\ne0\\x+3\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne-1\\x\ne-3\end{matrix}\right.\)
21: \(\dfrac{2x+7}{x^2+x-2}\)
ĐKXĐ: \(x^2+x-2\ne0\)
=>\(\left(x+2\right)\left(x-1\right)\ne0\)
=>\(\left\{{}\begin{matrix}x+2\ne0\\x-1\ne0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\ne-2\\x\ne1\end{matrix}\right.\)
Vậy: \(x\notin\left\{-2;1\right\}\)

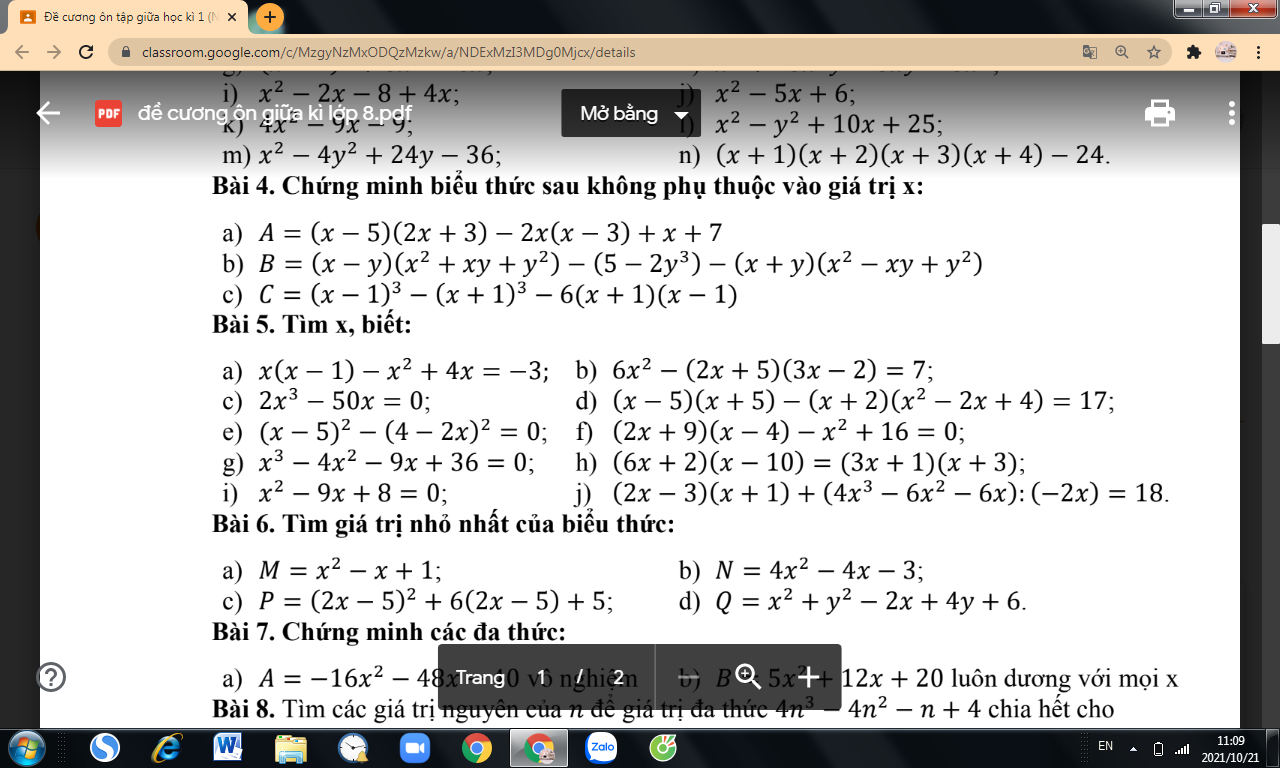
 giúp em với ạ bài 8 câu 2,113,15,21
giúp em với ạ bài 8 câu 2,113,15,21






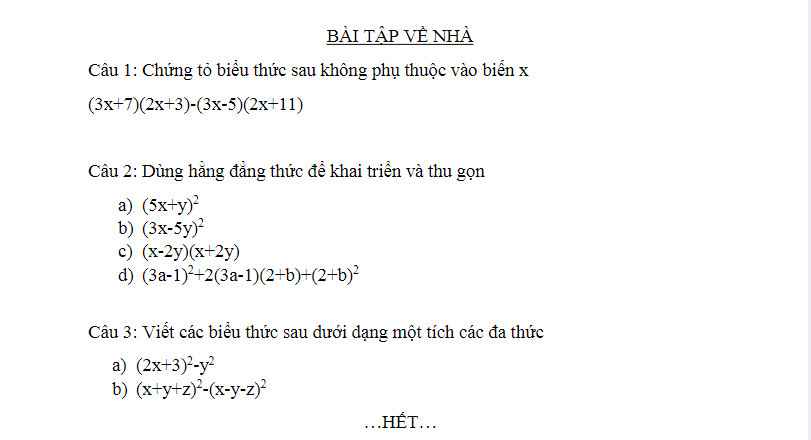

 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(