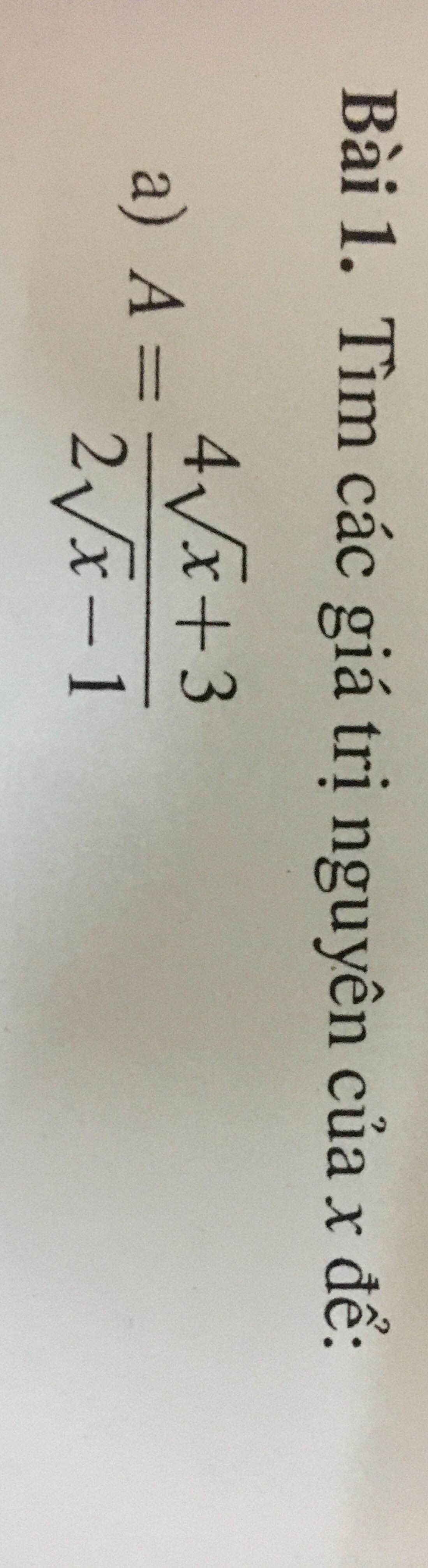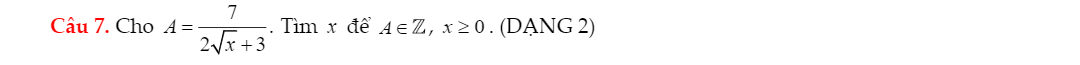ĐK: \(x\ge0;x\ne\dfrac{1}{4}\)
\(A=\dfrac{4\sqrt{x}+3}{2\sqrt{x}-1}\in Z\)
\(\Leftrightarrow\dfrac{2\left(2\sqrt{x}-1\right)+5}{2\sqrt{x}-1}\in Z\)
\(\Leftrightarrow2+\dfrac{5}{2\sqrt{x}-1}\in Z\)
\(\Leftrightarrow2\sqrt{x}-1\inƯ_5=\left\{\pm1;\pm5\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;2;6\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
\(\Leftrightarrow x\in\left\{0;1;9\right\}\)
Để A là số nguyên thì \(4\sqrt{x}+3⋮2\sqrt{x}-1\)
\(\Leftrightarrow5⋮2\sqrt{x}-1\)
\(\Leftrightarrow2\sqrt{x}-1\in\left\{-1;1;5\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;2;6\right\}\)
hay \(x\in\left\{0;1;9\right\}\)
`ĐKXĐ: x>=0; x\ne1/4`
`A=(4\sqrt{x}+3)/(2\sqrt{x}-1)`
`A=(4\sqrt{x}-2+5)/(2\sqrt{x}-1)`
`A=(4\sqrt{x}-2)/(2\sqrt{x}-1)+5/(2\sqrt{x}-1)`
`A=(2(2\sqrt{x}-1))/(2\sqrt{x}-1)+5/(2\sqrt{x}-1)`
`A=2+5/(2\sqrt{x}+1)`
Để `A` có giá trị nguyên `<=>2\sqrt{x}-1inƯ(5)={+-1; +-5}` và `x` có giá trị nguyên
Với `2\sqrt{x}-1=-5<=>\sqrt{x}=-2(VL)`
Với `2\sqrt{x}-1=-1<=>x=0(TM)`
Với `2\sqrt{x}-1=1<=>x=1(TM)`
Với `2\sqrt{x}-1=5<=>x=9(TM)`
Vậy `x in{0; 1; 9}` thì `A` có giá trị nguyên