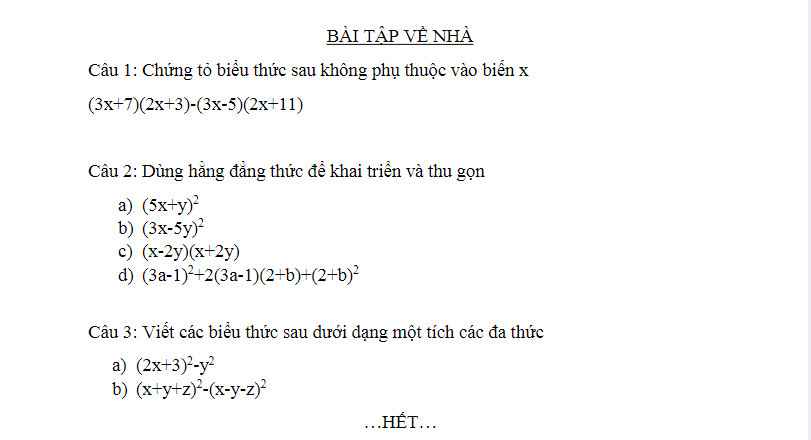a: Xét ΔABD vuông tại A và ΔHBI vuông tại H có
\(\hat{ABD}=\hat{HBI}\) (BD là phân giác của góc ABC)
Do đó: ΔABD~ΔHBI
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\hat{HAB}=\hat{HCA}\left(=90^0-\hat{HBA}\right)\)
Do đó: ΔHAB~ΔHCA
=>\(\frac{HA}{HC}=\frac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
\(HA^2=HB\cdot HC=9\cdot16=144=12^2\)
=>HA=12(cm)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(AB^2=12^2+9^2=144+81=225=15^2\)
=>AB=15(cm)
c: ΔBAD~ΔBHI
=>\(\hat{BDA}=\hat{BIH}\)
mà \(\hat{BIH}=\hat{AID}\) (hai góc đối đỉnh)
nên \(\hat{AID}=\hat{ADI}\)
=>ΔAID cân tại A
=>AI=AD
Xét ΔBAH có BI là phân giác
nên \(\frac{IA}{IH}=\frac{BA}{BH}\) (1)
Xét ΔBAC có BD là phân giác
nên \(\frac{BC}{BA}=\frac{DC}{DA}\left(2\right)\)
Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\hat{HBA}\) chung
Do đó: ΔBHA~ΔBAC
=>\(\frac{BH}{BA}=\frac{BA}{BC}\)
=>\(\frac{BC}{BA}=\frac{BA}{BH}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\frac{IA}{IH}=\frac{DC}{DA}\)
=>\(DC\cdot IH=AD\cdot AI=AD^2\)
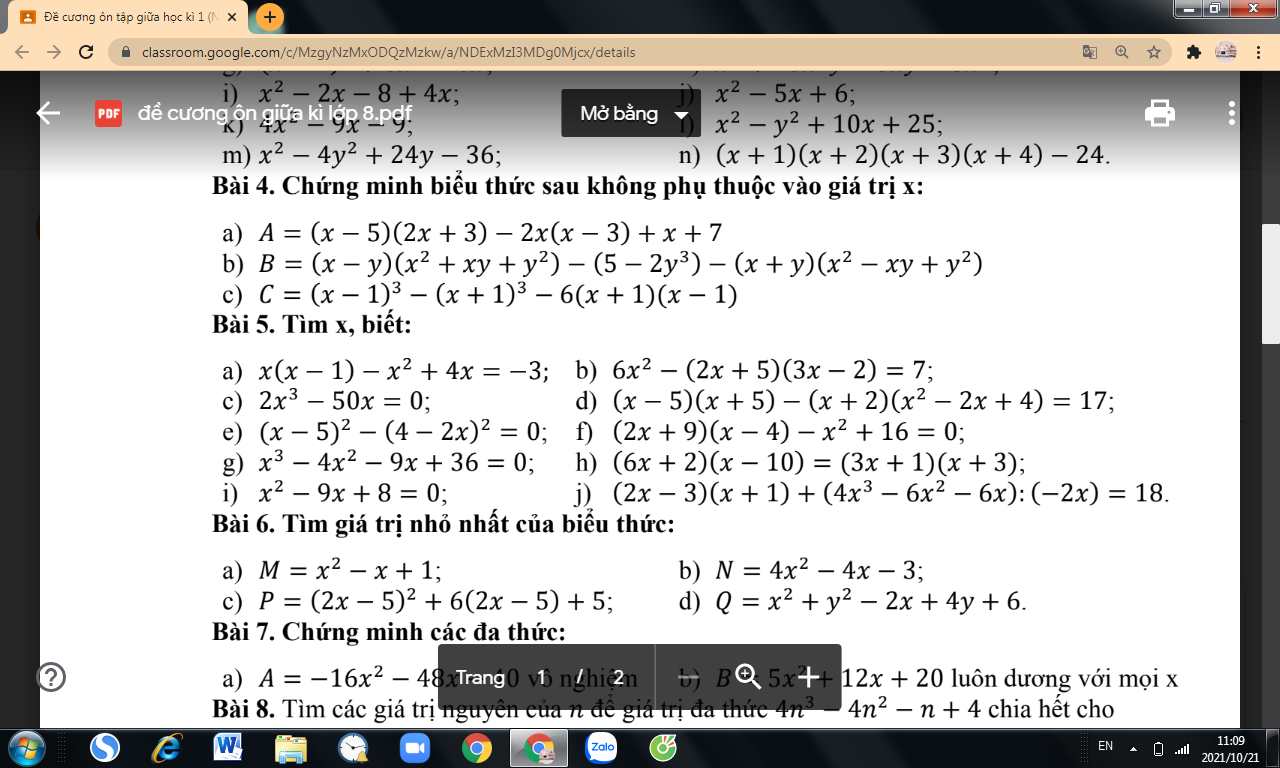
d: Xét ΔDKC vuông tại K và ΔDAB vuông tại A có
\(\hat{KDC}=\hat{ADB}\) (hai góc đối đỉnh)
Do đó: ΔDKC~ΔDAB
=>\(\frac{DK}{DA}=\frac{DC}{DB}\)
=>\(\frac{DK}{DC}=\frac{DA}{DB}\)
Xét ΔDKA và ΔDCB có
\(\frac{DK}{DC}=\frac{DA}{DB}\)
góc KDA=góc CDB
Do đó: ΔDKA~ΔDCB
=>\(\hat{DAK}=\hat{DBC}\)
mà \(\hat{DBC}=\hat{ABD}\) (BD là phân giác của góc ABC)
nên \(\hat{DAK}=\hat{ABD}\) (4)
ΔDAB~ΔDKC
=>\(\hat{DBA}=\hat{DCK}\left(5\right)\)
Từ (4),(5) suy ra \(\hat{DCK}=\hat{DAK}\)
=>\(\hat{KAC}=\hat{KCA}\)
=>ΔKAC cân tại K
mà KP là đường cao
nên P là trung điểm của AC
ΔABC vuông tại A
mà AQ là đường trung tuyến
nên QA=QB=QC
Ta có: QA=QC
=>Q nằm trên đường trung trực của AC(6)
Ta có: PA=PC
=>P nằm trên đường trung trực của AC(7)
Ta có: KA=KC
=>K nằm trên đường trung trực của AC(8)
Từ (6),(7),(8) suy ra Q,P,K thẳng hàng