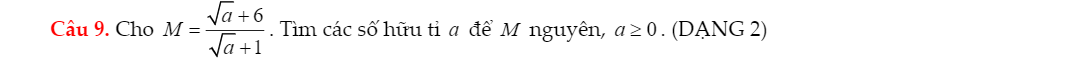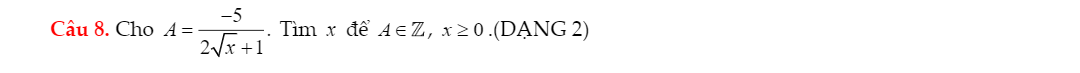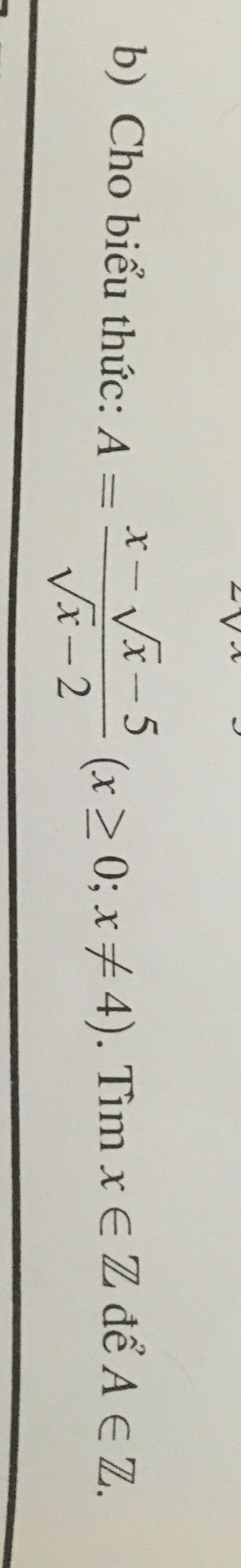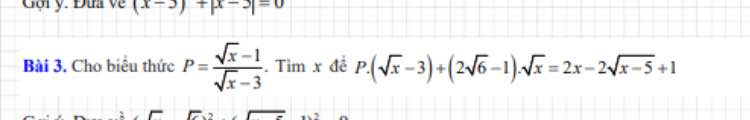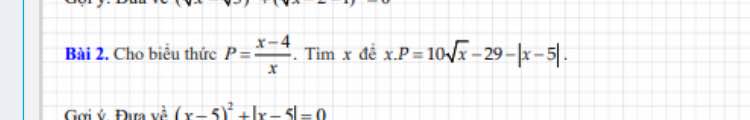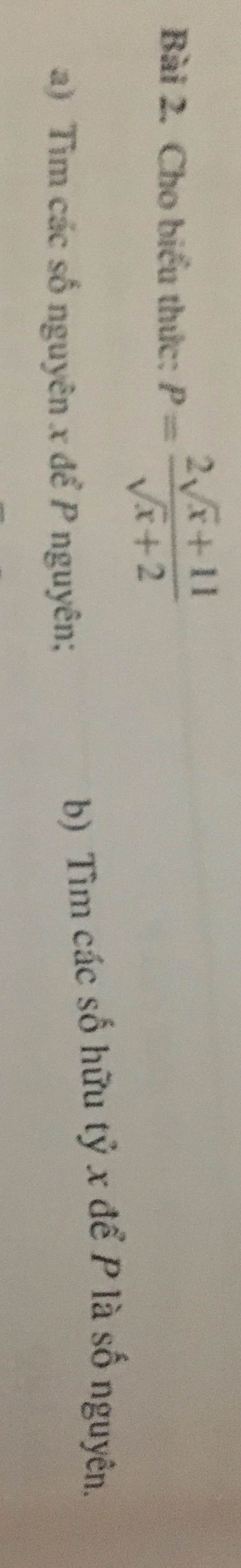\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2\left(\sqrt{x}+1\right)}{\sqrt{x}+1}-\dfrac{3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\)
Do \(\sqrt{x}+1\ge1\Rightarrow\dfrac{3}{\sqrt{x}+1}\le3\Rightarrow-\dfrac{3}{\sqrt{x}+1}\ge-3\)
\(\Rightarrow\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\ge2-3=-1\)
\(min=-1\Leftrightarrow x=0\)
Đúng 1
Bình luận (0)