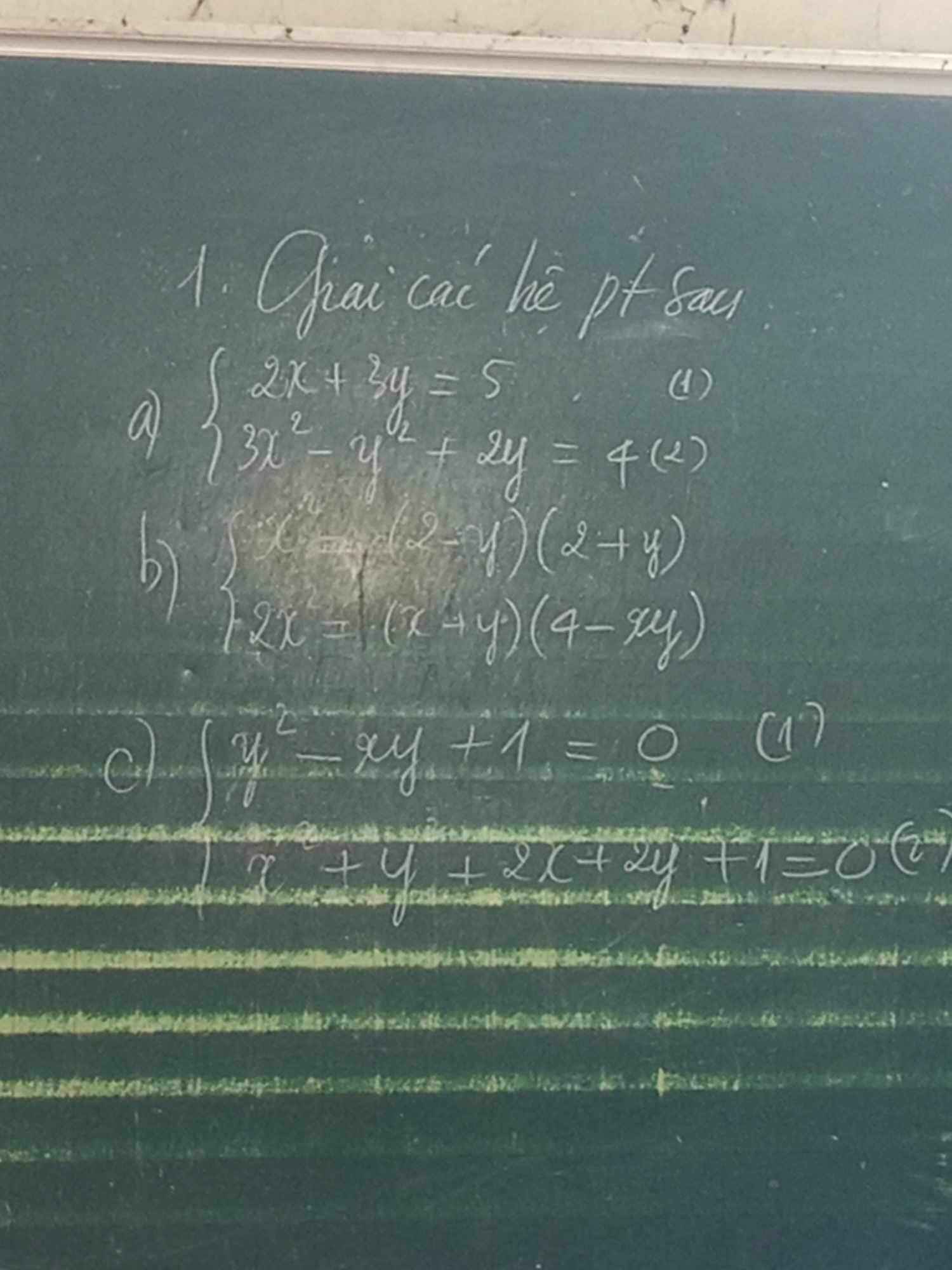a: 2x+3y=5
=>3y=5-2x
=>\(y=\frac53-\frac23x\)
\(3x^2-y^2+2y=4\)
=>\(3x^2-\left(\frac53-\frac23x\right)^2+2\left(\frac53-\frac23x\right)=4\)
=>\(3x^2-\left(\frac49x^2-\frac{20}{9}x+\frac{25}{9}\right)+\frac{10}{3}-\frac43x=4\)
=>\(3x^2-\frac49x^2+\frac{20}{9}x-\frac{25}{9}+\frac{10}{3}-\frac43x-4=0\)
=>\(\frac{23}{9}x^2+\frac89x-\frac{31}{9}=0\)
=>\(23x^2+8x-31=0\)
=>\(23x^2+31x-23x-31=0\)
=>x(23x+31)-(23x+31)=0
=>(23x+31)(x-1)=0
=>\(\left[\begin{array}{l}23x+31=0\\ x-1=0\end{array}\right.\Rightarrow\left[\begin{array}{l}23x=-31\\ x=1\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-\frac{31}{23}\\ x=1\end{array}\right.\)
Khi \(x=-\frac{31}{23}\) thì \(y=\frac53-\frac23\cdot\frac{-31}{23}=\frac53+\frac{62}{69}=\frac{59}{23}\)
Khi x=1 thì \(y=\frac53-\frac23x=\frac53-\frac23=\frac33=1\)
c: Ta có: \(\begin{cases}y^2-xy+1=0\\ x^2+y^2+2x+2y+1=0\end{cases}\)
=>\(x^2+y^2+2x+2y+1-y^2+xy-1=0\)
=>\(x^2+2x+2y\) +xy=0
=>x(x+2)+y(x+2)=0
=>(x+2)(x+y)=0
=>\(\left[\begin{array}{l}x+2=0\\ x+y=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=-2\\ y=-x\end{array}\right.\)
TH1: x=-2
\(y^2-xy+1=0\)
=>\(y^2-y\cdot\left(-2\right)+1=0\)
=>\(y^2+2y+1=0\)
=>\(\left(y+1\right)^2=0\)
=>y+1=0
=>y=-1
TH2: y=-x
\(y^2-xy+1=0\)
=>\(\left(-x\right)^2-x\cdot\left(-x\right)+1=0\)
=>\(2x^2+1=0\) (vô lý)
Vậy: (x;y)=(-2;-1)