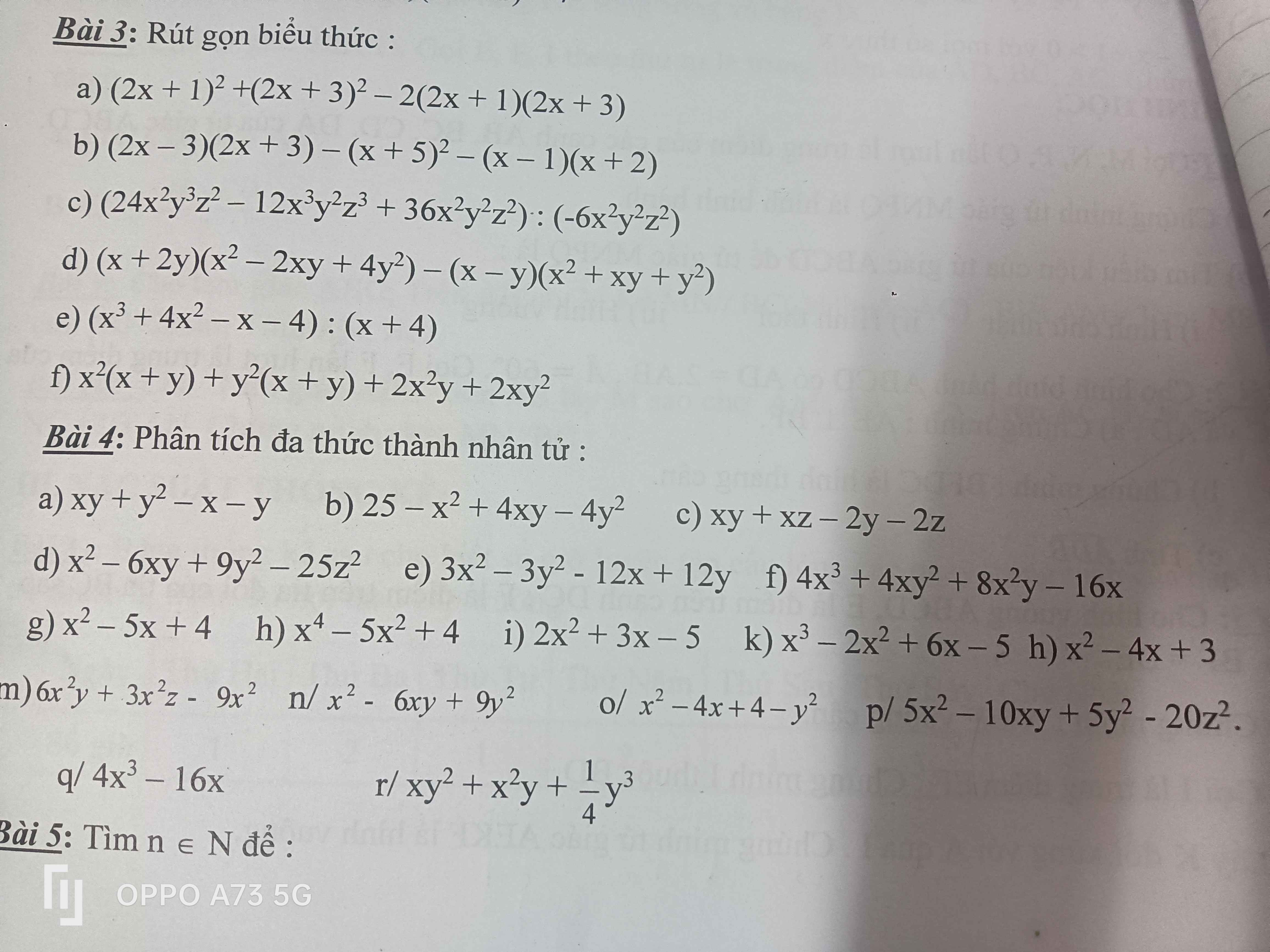Bài 4:
a: \(xy+y^2-x-y\)
\(=y\left(x+y\right)-\left(x+y\right)\)
=(x+y)(y-1)
b: \(25-x^2+4xy-4y^2\)
\(=25-\left(x^2-4xy+4y^2\right)\)
\(=25-\left(x-2y\right)^2=\left(5-x+2y\right)\left(5+x-2y\right)\)
c: \(xy+xz-2y-2z=x\left(y+z\right)-2\left(y+z\right)\)
=(y+z)(x-2)
d: \(x^2-6xy+9y^2-25z^2\)
\(=\left(x^2-6xy+9y^2\right)-\left(5z\right)^2\)
\(=\left(x-3y\right)^2-\left(5z\right)^2=\left(x-3y-5z\right)\left(x-3y+5z\right)\)
e: \(3x^2-3y^2-12x+12y\)
\(=3\left\lbrack x^2-y^2-4x+4y\right\rbrack\)
\(=3\left\lbrack\left(x-y\right)\left(x+y\right)-4\left(x-y\right)\right\rbrack=3\left(x-y\right)\left(x+y-4\right)\)
f: \(4x^3+4xy^2+8x^2y-16x\)
\(=4x\cdot x^2+4x\cdot y^2+4x\cdot2xy-4x\cdot4\)
\(=4x\left(x^2+2xy+y^2-4\right)\)
\(=4x\left\lbrack\left(x+y\right)^2-4\right\rbrack=4x\left(x+y+2\right)\left(x+y-2\right)\)
g: \(x^2-5x+4\)
\(=x^2-x-4x+4\)
=x(x-1)-4(x-1)
=(x-1)(x-4)
h: \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)=\left(x^2-1\right)\left(x^2-4\right)=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)
i: \(2x^2+3x-5\)
\(=2x^2-2x+5x-5\)
=2x(x-1)+5(x-1)
=(x-1)(2x+5)
k: \(x^3-2x^2+6x-5\)
\(=x^3-x^2-x^2+x+5x-5\)
\(=x^2\left(x-1\right)-x\left(x-1\right)+5\left(x-1\right)=\left(x-1\right)\left(x^2-x+5\right)\)
h: \(x^2-4x+3\)
\(=x^2-x-3x+3\)
=x(x-1)-3(x-1)
=(x-1)(x-3)
m: \(6x^2y+3x^2z-9x^2\)
\(=3x^2\cdot2y+3x^2\cdot z-3x^2\cdot3=3x^2\left(2y+z-3\right)\)
n: \(x^2-6xy+9y^2=x^2-2\cdot x\cdot3y+\left(3y\right)^2=\left(x-3y\right)^2\)
o: \(x^2-4x+4-y^2\)
\(=\left(x^2-4x+4\right)-y^2\)
\(=\left(x-2\right)^2-y^2=\left(x-2-y\right)\left(x-2+y\right)\)
p: \(5x^2-10xy+5y^2-20z^2\)
\(=5\left(x^2-2xy+y^2-4z^2\right)\)
\(=5\left\lbrack\left(x-y\right)^2-\left(2z\right)^2\right\rbrack\)
=5(x-y-2z)(x-y+2z)
q: \(4x^3-16x=4x\cdot x^2-4x\cdot4\)
\(=4x\left(x^2-4\right)=4x\left(x-2\right)\left(x+2\right)\)
r: \(xy^2+x^2y+\frac14y^3=y\cdot xy+y\cdot x^2+y\cdot\frac14y^2\)
\(=y\left(x^2+xy+\frac14y^2\right)=y\left(x+\frac12y\right)^2\)
Bài 3:
a: \(\left(2x+1\right)^2+\left(2x+3\right)^2-2\left(2x+1\right)\left(2x+3\right)\)
\(=\left(2x+3-2x-1\right)^2=2^2=4\)
b: \(\left(2x-3\right)\left(2x+3\right)-\left(x+5\right)^2-\left(x-1\right)\left(x+2\right)\)
\(=4x^2-9-\left(x^2+10x+25\right)-\left(x^2+2x-x-2\right)\)
\(=4x^2-9-x^2-10x-25-x^2+x+2=2x^2-9x-32\)
c: \(\left(24x^2y^3z^2-12x^3y^2z^3+36x^2y^2z^2\right):\left(-6x^2y^2z^2\right)\)
\(=-\frac{24x^2y^3z^2}{6x^2y^2z^2}+\frac{12x^3y^2z^3}{6x^2y^2z^2}-\frac{36x^2y^2z^2}{6x^2y^2z^2}\)
=-4y+2xy-6
d: \(\left(x+2y\right)\left(x^2-2xy+4y^2\right)-\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=\left\lbrack x^3+\left(2y\right)^3\right\rbrack-\left\lbrack x^3-y^3\right\rbrack\)
\(=x^3+8y^3-x^3+y^3=9y^3\)
e: \(\left(x^3+4x^2-x-4\right):\left(x+4\right)=\frac{x^2\left(x+4\right)-\left(x+4\right)}{x+4}=x^2-1\)
f: \(x^2\left(x+y\right)+y^2\left(x+y\right)+2x^2y+2xy^2\)
\(=\left(x+y\right)\left(x^2+y^2\right)+2xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2+y^2+2xy\right)=\left(x+y\right)\left(x+y\right)^2=\left(x+y\right)^3=x^3+3x^2y+3xy^2+y^3\)