Áp dụng tc dtsbn:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2x+2y+2z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\\ \Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.;\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2z\end{matrix}\right.\\ \Rightarrow P=\dfrac{xyz}{2x\cdot2y\cdot2z}=\dfrac{1}{8}\)
Chọn D
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\Rightarrow\left\{{}\begin{matrix}2y+z-x=2x\\2z-y+x=2y\\2x+y-z=2z\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2y+z=3x\\2z+x=3y\\2x+y=3z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-2y=z\\3y-2z=x\\3z-2x=y\end{matrix}\right.\) và \(\left\{{}\begin{matrix}3x-z=2y\\3y-x=2z\\3z-y=2x\end{matrix}\right.\)
Thay vào A:
\(A=\dfrac{z.x.y}{2y.2z.2x}=\dfrac{1}{8}\)
Vì x>0, y>0, z>0 ⇒ x+y+z>0
Áp dụng t/c dtsbn ta có:
\(\dfrac{2y+z-x}{x}=\dfrac{2z-y+x}{y}=\dfrac{2x+y-z}{z}=\dfrac{2y+z-x+2z-y+x+2x+y-z}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)
\(\dfrac{2y+z-x}{x}=2\Rightarrow2y+z-x=2x\Rightarrow2y+z=3x\\ \dfrac{2z-y+x}{y}=2\Rightarrow2z-y+x=2y\Rightarrow2z+x=3y\\ \dfrac{2x+y-z}{z}=2\Rightarrow2x+y-z=2z\Rightarrow2x+y=3z\)
\(A=\dfrac{\left(3x-2y\right)\left(3y-2z\right)\left(3z-2x\right)}{\left(3x-z\right)\left(3y-x\right)\left(3z-y\right)}\)
\(\Rightarrow A=\dfrac{\left(2y+z-2y\right)\left(2z+y-2z\right)\left(2x+y-2x\right)}{\left(2y+z-z\right)\left(2z+x-x\right)\left(2x+y-y\right)}\)
\(\Rightarrow A=\dfrac{xyz}{2x.2y.2z}\)
\(\Rightarrow A=\dfrac{1}{8}\)
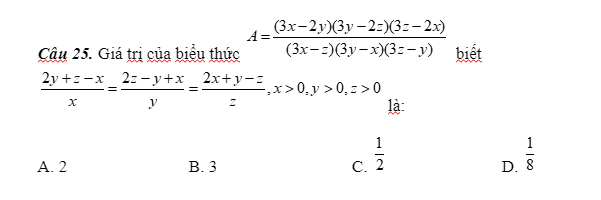
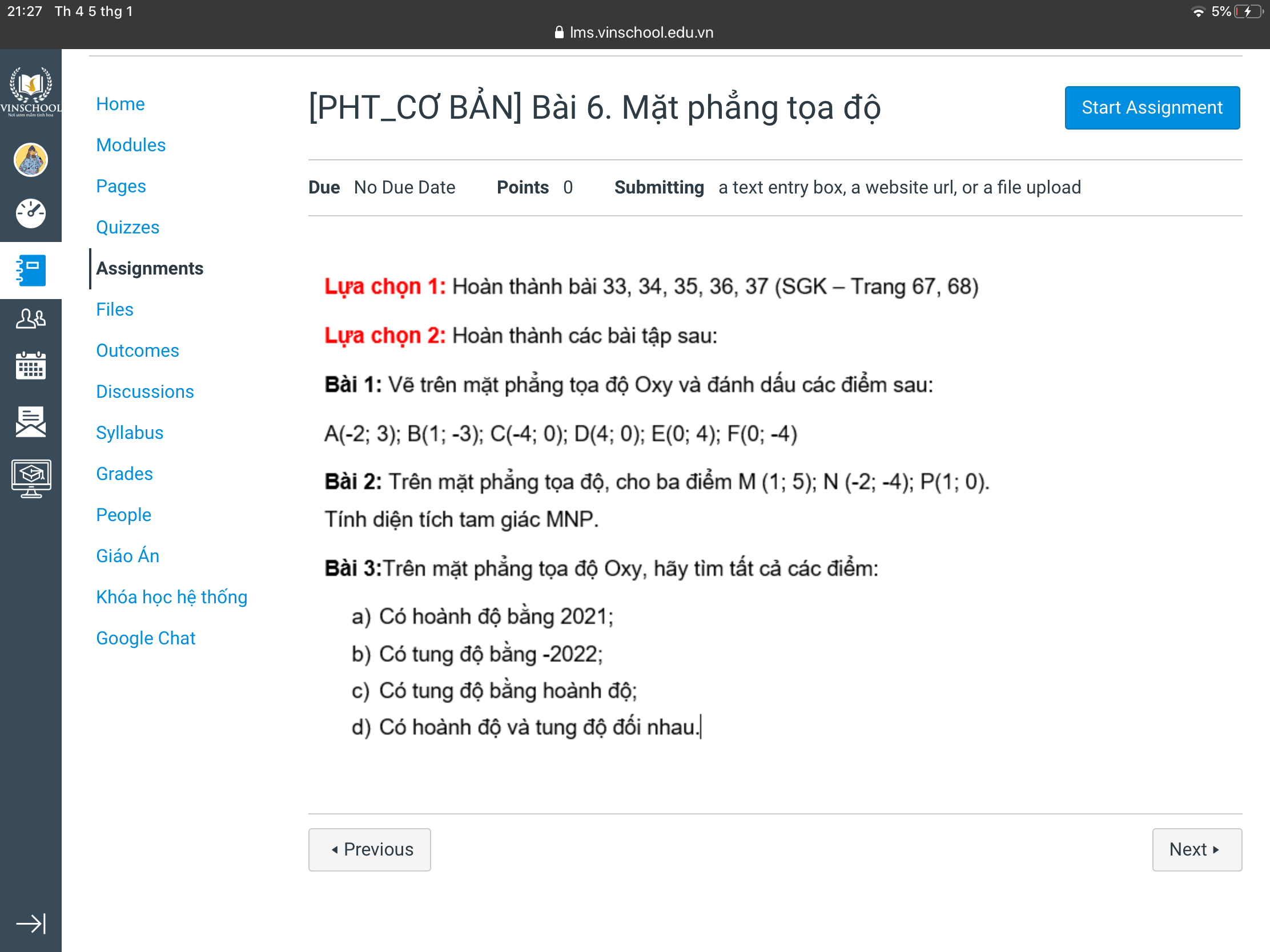Làm giúp e câu 3 với ạ🥺