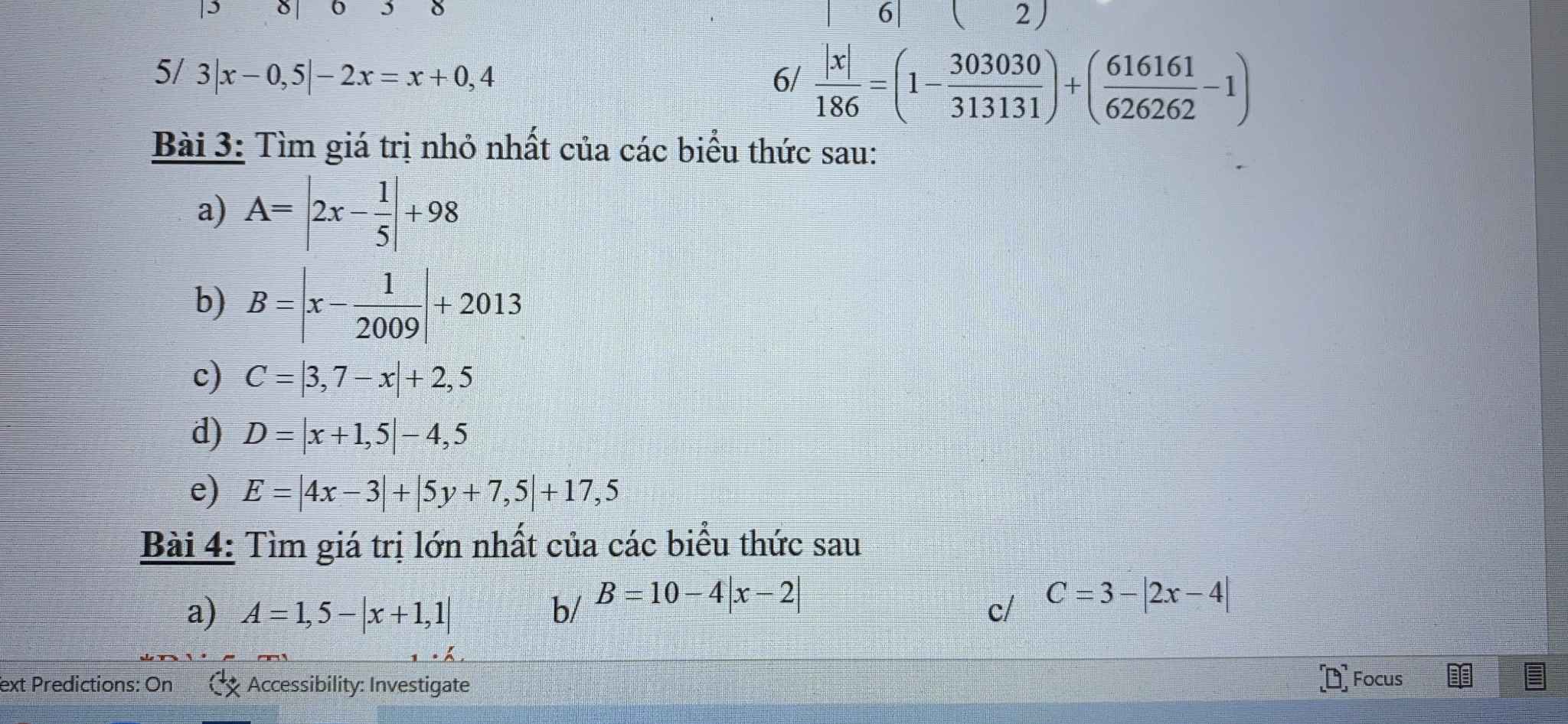
`a)A=(n+8)/(n-6)=((n-6)+14)/(n-6)`
`=1+14/(n-6)`
Để A nguyên thì 14 ⋮ n - 6
=> n - 6 ∈ Ư(14) = {1; -1; 2; -2; 7; -7; 14; -14}
=> n ∈ {7; 5; 8; 4; 13; -1; 20; -8}
`b)B=(4n+5)/(2n-3)=((4n-6)+11)/(2n-3)`
`=(2(2n-3)+11)/(2n-3)=2+11/(2n-3)`
Để B nguyên thì: 11 ⋮ 2n - 3
=> 2n - 3 ∈ Ư(11) = {1; -1; 11; -11}
=> 2n ∈ {4; 2; 14; -8}
=> n ∈ {2; 1; 7; -4}
Phần a:
Để \( A \) là một số nguyên, ta cần \( n + 8 \) phải chia hết cho \( n + 6 \). Ta viết lại biểu thức:
\[
A = \frac{n + 6 + 2}{n + 6} = 1 + \frac{2}{n + 6}
\]
Để \( A \) là một số nguyên, \(\frac{2}{n + 6}\) phải là một số nguyên, nghĩa là \( n + 6 \) phải là ước của 2. Các ước của 2 là \( \pm 1, \pm 2 \).
- Nếu \( n + 6 = 1 \), thì \( n = -5 \).
- Nếu \( n + 6 = -1 \), thì \( n = -7 \).
- Nếu \( n + 6 = 2 \), thì \( n = -4 \).
- Nếu \( n + 6 = -2 \), thì \( n = -8 \).
Vậy \( n = -5, -7, -4, -8 \) là các giá trị \( n \) làm cho \( A \) đạt giá trị nguyên.
Phần b:
Để \( B \) là một số nguyên, ta cần \( 4n + 5 \) phải chia hết cho \( 2n - 3 \). Ta viết lại biểu thức:
\[
B = \frac{4n + 5}{2n - 3} = 2 + \frac{11}{2n - 3}
\]
Để \( B \) là một số nguyên, \(\frac{11}{2n - 3}\) phải là một số nguyên, nghĩa là \( 2n - 3 \) phải là ước của 11. Các ước của 11 là \( \pm 1, \pm 11 \).
- Nếu \( 2n - 3 = 1 \), thì \( 2n = 4 \) và \( n = 2 \).
- Nếu \( 2n - 3 = -1 \), thì \( 2n = 2 \) và \( n = 1 \).
- Nếu \( 2n - 3 = 11 \), thì \( 2n = 14 \) và \( n = 7 \).
- Nếu \( 2n - 3 = -11 \), thì \( 2n = -8 \) và \( n = -4 \).
Vậy \( n = 2, 1, 7, -4 \) là các giá trị \( n \) làm cho \( B \) đạt giá trị nguyên.








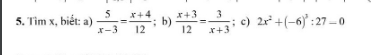




 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ


 Tớ Đang Cần giải bài này gấp mai tớ phải gửi bài giúp tớ với
Tớ Đang Cần giải bài này gấp mai tớ phải gửi bài giúp tớ với