Question

Giải tam giác ABC vuông tại A có AC =15cm , góc BCA = 20 độ.

Answer 1

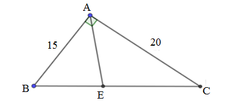
Ta có: ΔABC vuông tại A

nên \(\widehat{B}+\widehat{C}=90^0\)

hay \(\widehat{B}=70^0\)

Xét ΔABC vuông tại A có 

\(AB=AC\cdot\tan20^0\simeq5,46\left(cm\right)\)

\(\Leftrightarrow BC\simeq15,96\left(cm\right)\)

Answer 2

\(\cos\widehat{BCA}=\dfrac{AC}{BC}\Rightarrow BC=AC:cosBCA=15:cos20^0\simeq15,9cm\)

\(AB=\sqrt{BC^2-AC^2}=\sqrt{15,9^2-15^2}\simeq5,3cm\)

\(ABC=BAC-BCA=90^0-20^0=70^0\)