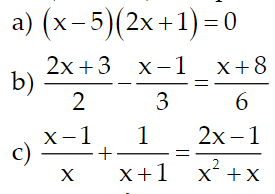a) \(\left(x-5\right)\left(2x+1\right)=0\)
\(\Rightarrow x-5=0\) hay \(2x+1=0\)
\(\Rightarrow x=5\) \(2x=-1\)
\(\Rightarrow\) \(x=-\dfrac{1}{2}\)
Vậy : S = {5; \(-\dfrac{1}{2}\)}
b) \(\dfrac{2x+3}{2}-\dfrac{x-1}{3}=\dfrac{x+8}{6}\)
\(\Leftrightarrow\dfrac{3\left(2x+3\right)}{6}-\dfrac{2\left(x-1\right)}{6}=\dfrac{x+8}{6}\)
\(\Leftrightarrow3\left(2x+3\right)-2\left(x-1\right)=x+8\)
\(\Leftrightarrow6x+9-2x+2=x+8\)
\(\Leftrightarrow6x-2x-x=8-9-2\)
\(\Leftrightarrow3x=-3\)
\(\Leftrightarrow x=-1\)
Vậy : S = {-1}
\(a,\left(x-5\right)\left(2x-1\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x-5=0\\2x-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=5\\x=\dfrac{1}{2}\end{matrix}\right.\)
\(b,\dfrac{2x+3}{2}-\dfrac{x+1}{3}=\dfrac{x+8}{6}\)
\(\Rightarrow\)\(\dfrac{6x+9}{6}-\dfrac{2x+2}{6}=\dfrac{x+8}{6}\)
\(\Rightarrow\)\(\dfrac{4x-7}{6}=\dfrac{x+8}{6}\Rightarrow4x-7=x+8\)
\(\Rightarrow3x=15\Rightarrow x=5\)
\(c,\dfrac{x-1}{x}+\dfrac{1}{x+1}=\dfrac{2x-1}{x^2+x}\)
\(\Rightarrow\)\(\dfrac{\left(x-1\right).\left(x+1\right)}{x\left(x+1\right)}+\dfrac{x}{x\left(x+1\right)}=\dfrac{2x-1}{x^2+x}\)
\(\Rightarrow\)\(\dfrac{x^2-1+x}{x^2+x}=\dfrac{2x-1}{x^2+x}\)
\(\Rightarrow x^2+x-1=2x-1\)
\(\Rightarrow x^2=x\Rightarrow x=0;1\)
\(a,\left(x-5\right)\left(2x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\2x+1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=-\dfrac{1}{2}\end{matrix}\right.\\ b,\dfrac{2x+3}{2}-\dfrac{x-1}{3}=\dfrac{x+8}{6}\\ \Leftrightarrow\dfrac{3\left(2x+3\right)}{6}-\dfrac{2\left(x-1\right)}{6}-\dfrac{x+8}{6}=0\\ \Leftrightarrow6x+9-2x+2-x-8=0\\ \Leftrightarrow3x+3=0\\ \Leftrightarrow x=-1\)
\(c,ĐKXĐ:\left\{{}\begin{matrix}x\ne0\\x\ne-1\end{matrix}\right.\\ \dfrac{x-1}{x}+\dfrac{1}{x+1}=\dfrac{2x-1}{x^2+x}\\ \Leftrightarrow\dfrac{\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}+\dfrac{x}{x\left(x+1\right)}-\dfrac{2x-1}{x\left(x+1\right)}=0\)
\(\Rightarrow x^2-1+x-2x+1=0\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
c) \(\dfrac{x-1}{x}+\dfrac{1}{x+1}=\dfrac{2x-1}{x^2+x}\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x-1\right)}{x^2+x}+\dfrac{x}{x^2+x}=\dfrac{2x-1}{x^2+x}\)
\(\Leftrightarrow\left(x+1\right)\left(x-1\right)+x=2x-1\)
\(\Leftrightarrow x^2-x+x-1+x-2x+1=0\)
\(\Leftrightarrow x^2-x=0\)
\(\Leftrightarrow x\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(a,\left(x-5\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x-5=0\\2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=5\\2x=-1\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x=5\\x=-\dfrac{1}{2}\end{matrix}\right.\)
\(Vậy^{ }_{ }S=\left\{5;-\dfrac{1}{2}\right\}\)
\(b,\dfrac{2x+3}{2}-\dfrac{x-1}{3}=\dfrac{x+8}{6}\)
\(\Leftrightarrow\dfrac{\left(2x+3\right)3}{6}-\dfrac{x-1}{6}=\dfrac{x+8}{6}\)
\(\Leftrightarrow\left(2x+3\right)3-x-1=x+8\)
\(\Leftrightarrow6x+9-x-1=x+8\)
\(\Leftrightarrow6x-x-x=8-9+1\)
\(\Leftrightarrow4x=0\)
\(\Leftrightarrow x=0\)
\(Vậy\) \(S=\left\{0\right\}\)
\(c,\dfrac{x-1}{x}+\dfrac{1}{x+1}=\dfrac{2x-1}{x^2+x}\)
\(\Rightarrow\)\(\dfrac{\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}+\dfrac{1x}{x\left(x+1\right)}=\dfrac{2x-1}{x\left(x+1\right)}\)
Điều kiện xác định là:
\(x\left(x+1\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne1\end{matrix}\right.\)
Vậy điều kiện x/đ là \(x\ne0\) và \(x\ne-1\)
\(\Leftrightarrow\left(x+1\right)\left(x-1\right)+1x=2x-1\)
\(\Leftrightarrow x^2-1+x=2x-1\)
\(\Leftrightarrow x^2-1+x-2x=-1\)
\(\Leftrightarrow x^2-1-x=-1\)
\(\Leftrightarrow x^2-1-x+1=0\)
\(\Leftrightarrow x^2-x=0\)
\(\Leftrightarrow x\left(x-1\right)=0\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(S=\left\{1\right\}\)