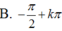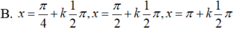`2sin x+cosx=0`
`<=> sinx + 1/2 cosx=0`
Có: `a^2+b^2=1^2+(1/2)^2=5/4 \ne 1`
`=>` PTVN.
\(2sinx+cosx=0\)
\(\Leftrightarrow\dfrac{2}{\sqrt{5}}.sinx+\dfrac{1}{\sqrt{5}}cosx=0\)
Đặt \(cos\alpha=\dfrac{2}{\sqrt{5}}\) và \(sin\alpha=\dfrac{1}{\sqrt{5}}\) (vì \(\left(\dfrac{2}{\sqrt{5}}\right)^2+\left(\dfrac{1}{\sqrt{5}}\right)^2=1\))
pttt: \(sinx.cos\alpha+cosx.sin\alpha=0\)
\(\Leftrightarrow sin\left(x+\alpha\right)=0\)
\(\Rightarrow x=-arc.sin\alpha+k\pi\left(k\in Z\right)\)
(phải không?)