2.sin x + cos x = 1
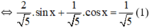
Vì 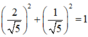 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 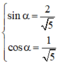
(1) trở thành:
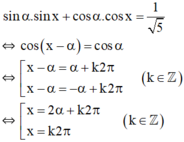
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn 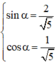
2.sin x + cos x = 1
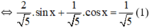
Vì 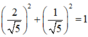 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 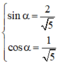
(1) trở thành:
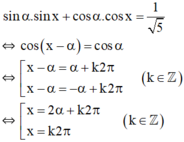
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z }
với α thỏa mãn 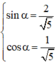
Giải phương trình (2cosx - 1)(2sinx + cosx) = sin2x - sinx
![]()
![]()
![]()
![]()
Giải phương trình sin x cos x + 2 sin x + cos x = 2
A. x = π 2 + k π x = k π , k ∈ ℤ .
B. x = π 2 + k 2 π x = k 2 π , k ∈ ℤ .
C. x = − π 2 + k 2 π x = k 2 π , k ∈ ℤ .
D. x = − π 2 + k π x = k π , k ∈ ℤ .
Nghiệm phương trình: cosx ( cosx + 2 sinx ) + 3 sinx ( sinx + 2 ) sin 2 x - 1 = 1
A. x = ± π 4 + k2π, k ∈ Z
B. x = - π 4 + kπ, k ∈ Z
C. x = - π 4 + k2π, x = - 3 π 4 + k2π, k ∈ Z
D. x = - π 4 + k2π, k ∈ Z
Nghiệm của phương trình 2 sin x ( cos x - 1 ) = 3 cos 2 x là:
A. π 3 + k 2 π , k ∈ ℤ hoặc 4 π 9 + k 2 π 3 , k ∈ ℤ
B. π 3 + k π , k ∈ ℤ hoặc 4 π 9 + k π 3 , k ∈ ℤ
C. - π 3 + k 2 π , k ∈ ℤ hoặc 2 π 9 + k 2 π 3 , k ∈ ℤ
D. - π 3 + k π , k ∈ ℤ hoặc 2 π 9 + k π 3 , k ∈ ℤ
Giải phương trình sau: cosx ( cosx + 2 sinx ) + 3 sinx ( sinx + 2 ) sin 2 x - 1 = 1
A. x = - π 4 + k2π
B. x = - 3 π 4 + k2π
C. x = ± π 4 + kπ
D. Cả A và B đúng
Cho phương trình: (2cosx-1)(2sinx+cosx)=sin2x-sinx.Tính tan của nghiệm x lớn nhất của phương trình trong khoảng - 2 π ; 2 π
A.-1
B.1
C.2
D. 2 2
Phương trình 2 sin x + cos x + 1 sin x - 2 cos x + 3 = m có nghiệm khi:
A. m ≥ 2 h o ặ c m ≤ - 1 2
B. - 2 ≤ m ≤ 1 2
C. - 1 2 ≤ m ≤ 2
D. - 1 2 < m < 2
Tìm m để phương trình m = cos x + 2 sin x + 3 2 cos x - sin x + 4 có nghiệm.
![]()
![]()
![]()
![]()
Cho x 0 là nghiệm của phương trình sin x . cos x + 2 sin x + c o s x = 2 thì giá trị của P = 3 + sin 2 x 0 là
A. 3
B. 2
C. 1
D. 4