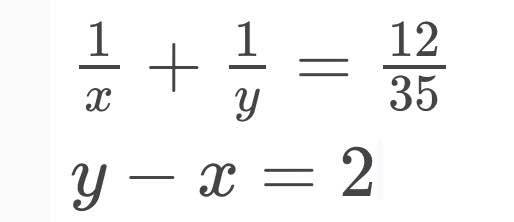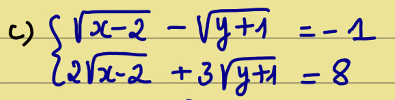Question

Giải hpt

Answer 1

\(\Leftrightarrow\begin{cases}\frac{x+y}{xyz}=\frac12\\ \frac{y+z}{xyz}=\frac56\\ \frac{x+z}{xyz}=\frac23\end{cases}\)

\(\Leftrightarrow\begin{cases}\frac{1}{yz}+\frac{1}{zx}=\frac12\\ \frac{1}{xy}+\frac{1}{xz}=\frac56\\ \frac{1}{xy}+\frac{1}{yz}=\frac23\end{cases}\) (1)

Cộng vế:

\(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{xz}=1\) (2)

Trừ vế của (2) cho từng pt của (1):

\(\Rightarrow\begin{cases}\frac{1}{xy}=\frac12\\ \frac{1}{yz}=\frac16\\ \frac{1}{zx}=\frac13\end{cases}\) \(\Rightarrow\begin{cases}xy=2\\ yz=6\\ zx=3\end{cases}\) (3)

Nhân vế với vế của (3) \(\Rightarrow xyz=\pm6\)

=>(x;y;z)=(2;1;3);(-2;-1;-3)