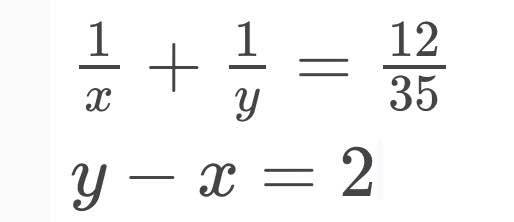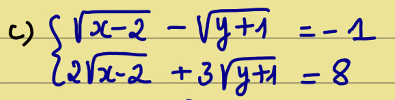Question

Giải hpt

Answer 1

\(\Leftrightarrow\begin{cases}x+xy+y+1=10\\ y+yz+z+1=5\\ z+xz+x+1=2\end{cases}\)

\(\Leftrightarrow\begin{cases}\left(x+1\right)\left(y+1\right)=10\\ \left(y+1\right)\left(z+1\right)=5\\ \left(z+1\right)\left(x+1\right)=2\end{cases}\) (1)

Nhân vế với vế của (1):

\(\Rightarrow\left(x+1\right)\left(y+1\right)\left(z+1\right)=\pm10\) (2)

Chia vế cho vế của (2) lần lượt cho (1):

\(\Rightarrow\begin{cases}x+1=2\\ y+1=5\\ z+1=1\end{cases}\) hoặc \(\begin{cases}x+1=-2\\ y+1=-5\\ z+1=-1\end{cases}\)