Ta có ( biểu diễn y theo x từ phương trình thứ hai):
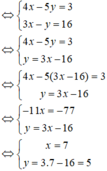
Vậy hệ phương trình có nghiệm duy nhất (7;5)
Ta có ( biểu diễn y theo x từ phương trình thứ hai):
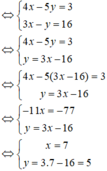
Vậy hệ phương trình có nghiệm duy nhất (7;5)
Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)
4 x − 5 y = 3 3 x − y = 16
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x + y 5 = 0 x 5 + 3 y = 1 − 5 b ) ( 2 − 3 ) x − 3 y = 2 + 5 3 4 x + y = 4 − 2 3
Giải hệ phương trình sau bằng phương pháp đồ thị và phương pháp thế
\(\left\{{}\begin{matrix}2x-y=5\\x+2y=5\end{matrix}\right.\)
giải hệ phương trình bằng phương pháp thế
\(\left\{{}\begin{matrix}\dfrac{x}{2}+\dfrac{y}{2}=1\\x+y=3\end{matrix}\right.\)
Giải các hệ phương trình sau bằng phương pháp thế: x - y = 3 3 x - 4 y = 2
Giải các hệ phương trình sau bằng phương pháp thế: x - 2 2 y = 5 x 2 + y = 1 - 10
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x − y = 3 3 x − 4 y = 2 b ) 7 x − 3 y = 5 4 x + y = 2 c ) x + 3 y = − 2 5 x − 4 y = 11
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x 2 − y 3 = 1 x + y 3 = 2 b ) x − 2 2 y = 5 x 2 + y = 1 − 10 c ) ( 2 − 1 ) x − y = 2 x + ( 2 + 1 ) y = 1
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ toạ độ. Xác định toạ độ giao điểm của hai đường thẳng
2x + y = 3
x-2y = 4