b: ΔAHB vuông tại H
=>\(AB^2=AH^2+HB^2\)
=>\(AH^2=13^2-5^2=144=12^2\)
=>AH=12(cm)
Xét ΔABH vuông tại H có \(sinB=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(cosB=\dfrac{BH}{AB}=\dfrac{5}{13}\)
\(tanB=\dfrac{AH}{HB}=\dfrac{12}{5}\)
\(cotB=\dfrac{HB}{AH}=\dfrac{5}{12}\)
Xét ΔABC vuông tại A có
\(cosC=sinB=\dfrac{12}{13}\)
\(sinC=cosB=\dfrac{5}{13}\)
\(cotC=tanB=\dfrac{12}{5}\)
\(tanC=cotB=\dfrac{5}{12}\)
c: BC=BH+CH=16+9=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC=16\cdot25=400=20^2\\AC^2=CH\cdot BC=9\cdot25=225=15^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=20\left(cm\right)\\AC=15\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(sinB=cosC=\dfrac{AC}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(cosB=sinC=\dfrac{AB}{BC}=\dfrac{20}{25}=\dfrac{4}{5}\)
\(tanB=cotC=\dfrac{AC}{AB}=\dfrac{15}{20}=\dfrac{3}{4}\)
\(cotB=tanC=\dfrac{AB}{AC}=\dfrac{20}{15}=\dfrac{4}{3}\)
d: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có
\(sinB=cosC=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(cosB=sinC=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(tanB=cotC=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\)
\(cotB=tanC=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\)










 Giải giúp tớ với ạ, tớ cần gấp lắm
Giải giúp tớ với ạ, tớ cần gấp lắm
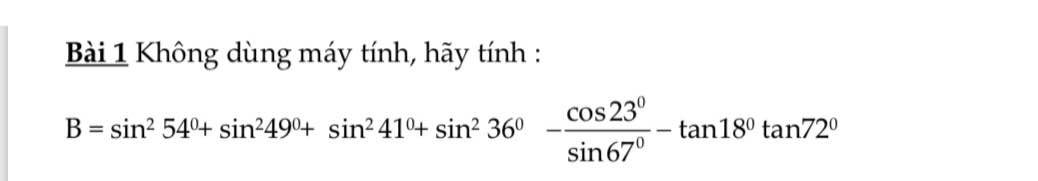


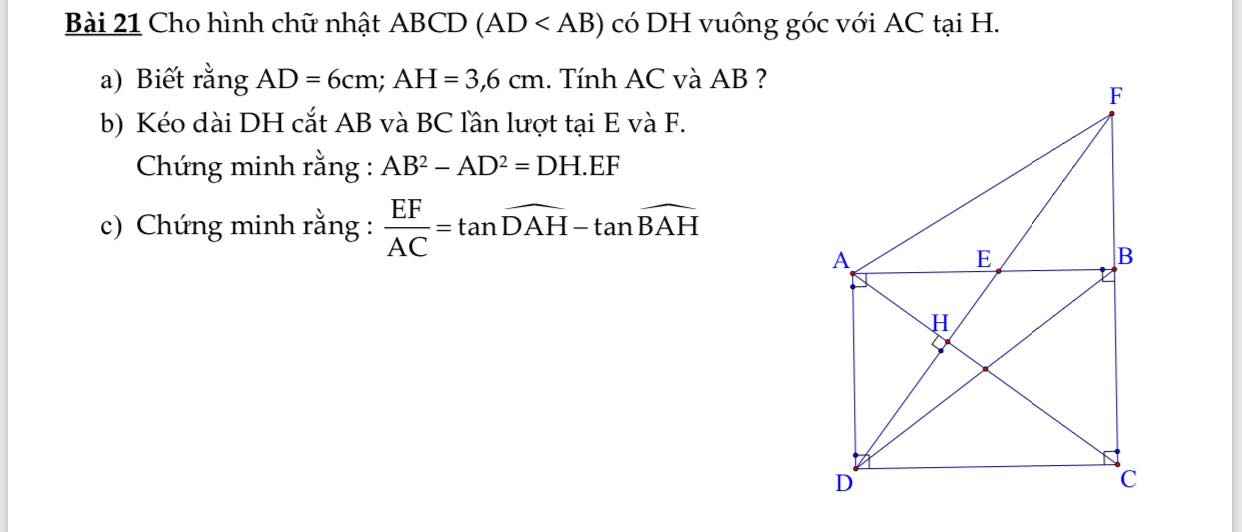




 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn