6B
\(a,3x\left(x-5\right)-x\left(3x-7\right)=16\\ \Leftrightarrow3x^2-15x-3x^2+7x=16\\ \Leftrightarrow-8x=16\\ \Leftrightarrow x=\dfrac{16}{-8}\\ \Leftrightarrow x=-2\\ b,-2x^2+3x+6+\left(\dfrac{5}{7}x\right)\left(\dfrac{14x}{5}+21\right)=9\\ \Leftrightarrow-2x^2+3x+6+2x^2+15x=9\\ \Leftrightarrow18x+6=9\\ \Leftrightarrow18x=9-6=3\\ \Leftrightarrow x=\dfrac{3}{18}\\ \Leftrightarrow x=\dfrac{1}{6}\\ c,\left(x+1\right)\left(4x+3\right)+\left(x+2\right)\left(x+3\right)=\left(5x-1\right)\left(x-1\right)+28\\ \Leftrightarrow\left(4x^2+3x+4x+3\right)+\left(x^2+2x+3x+6\right)=\left(5x^2-x-5x+1\right)+28\\ \Leftrightarrow4x^2+7x+3+x^2+5x+6=5x^2-6x+1+28\\ \Leftrightarrow5x^2+12x+9=5x^2-6x+29\\ \Leftrightarrow5x^2-5x^2+12x+6x=29-9\\ \Leftrightarrow18x=20\\ \Leftrightarrow x=\dfrac{20}{18}\\ \Leftrightarrow x=\dfrac{10}{9}\)
9B: \(15x^5y^3:B=5x^4y\)
=>\(B=\dfrac{15x^5y^3}{5x^4y}=\dfrac{15}{5}\cdot\dfrac{x^5}{x^4}\cdot\dfrac{y^3}{y}=3xy^2\)
10B: Để A,B đồng thời chia hết cho C thì
\(\left\{{}\begin{matrix}12\cdot x^{2n}y^{12-3n}⋮3x^3y^4\\3x^3y^7⋮3x^3y^4\left(đúng\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2n>=3\\12-3n>=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n>=\dfrac{3}{2}\\-3n>=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}n>=\dfrac{3}{2}\\n< =\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow n=2\)
11A:
a: \(A=\dfrac{15x^5y^3-10x^3y^2+20x^4y^4}{5x^2y}\)
\(=\dfrac{15x^5y^3}{5x^2y}-\dfrac{10x^3y^2}{5x^2y}+\dfrac{20x^4y^4}{5x^2y}\)
\(=3x^3y^2-2xy+4x^2y^3\)
Thay x=1;y=-2 vào A, ta được:
\(A=3\cdot1^3\cdot\left(-2\right)^2-2\cdot1\cdot\left(-2\right)+4\cdot1^2\cdot\left(-2\right)^3\)
=12+4-32
=16-32=-16
b: \(B=\dfrac{4x^4y^2+3x^4y^3-6x^3y^2}{-x^2y^2}=-\dfrac{4x^4y^2}{x^2y^2}-\dfrac{3x^4y^3}{x^2y^2}+\dfrac{6x^3y^2}{x^2y^2}\)
\(=-4x^2-3x^2y+6x\)
Thay x=-2;y=-2 vào B, ta được:
\(B=-4\cdot\left(-2\right)^2-3\cdot\left(-2\right)^2\cdot\left(-2\right)+6\cdot\left(-2\right)\)
\(=-4\cdot4+6\cdot4-12\)
=-16+12
=-4







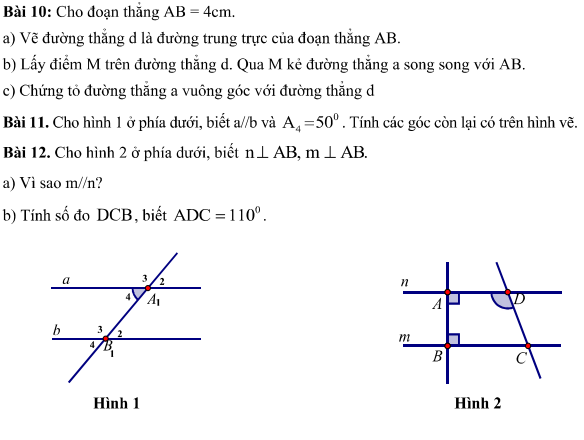







 giải giúp em với ạ
giải giúp em với ạ 
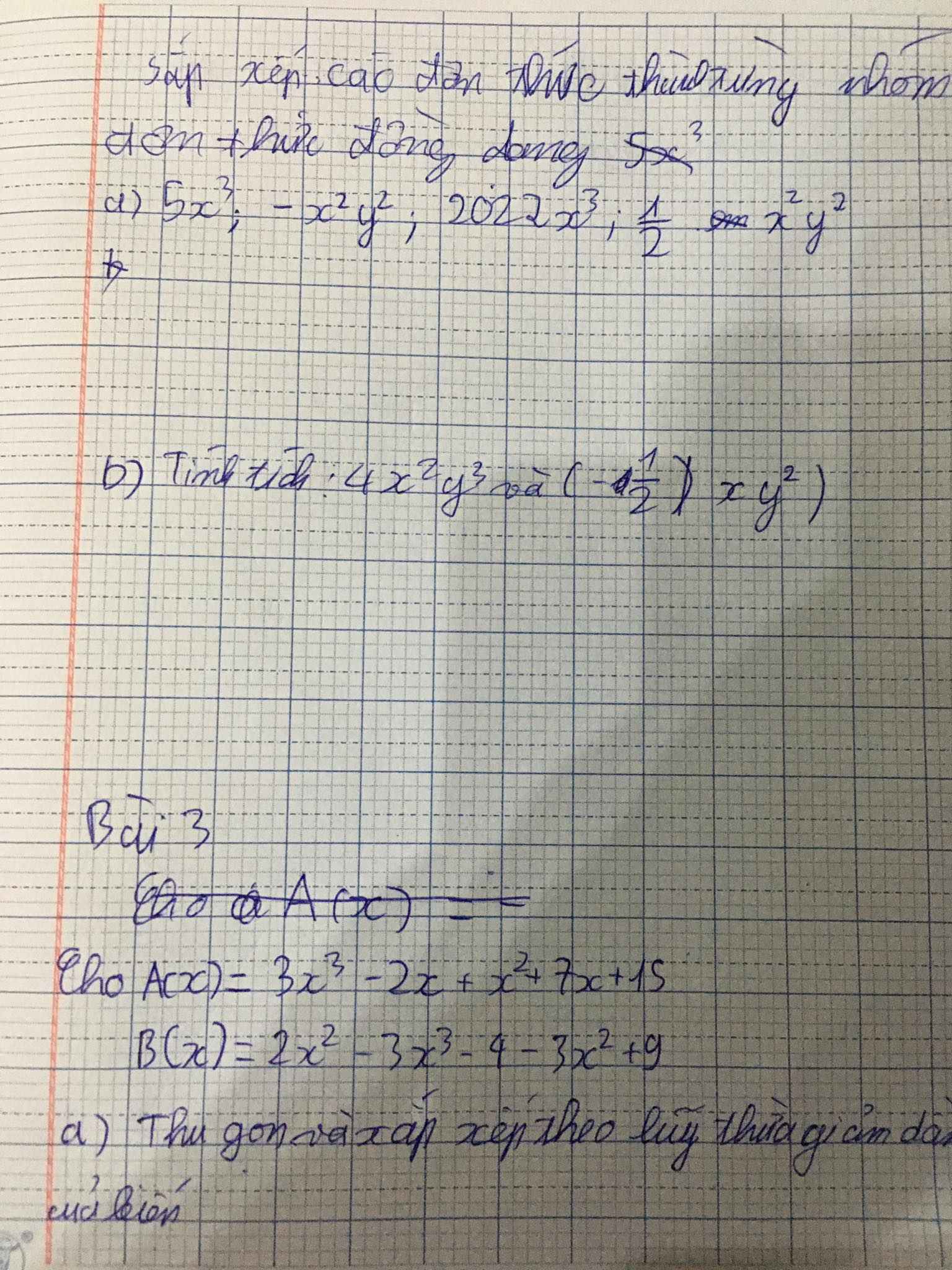

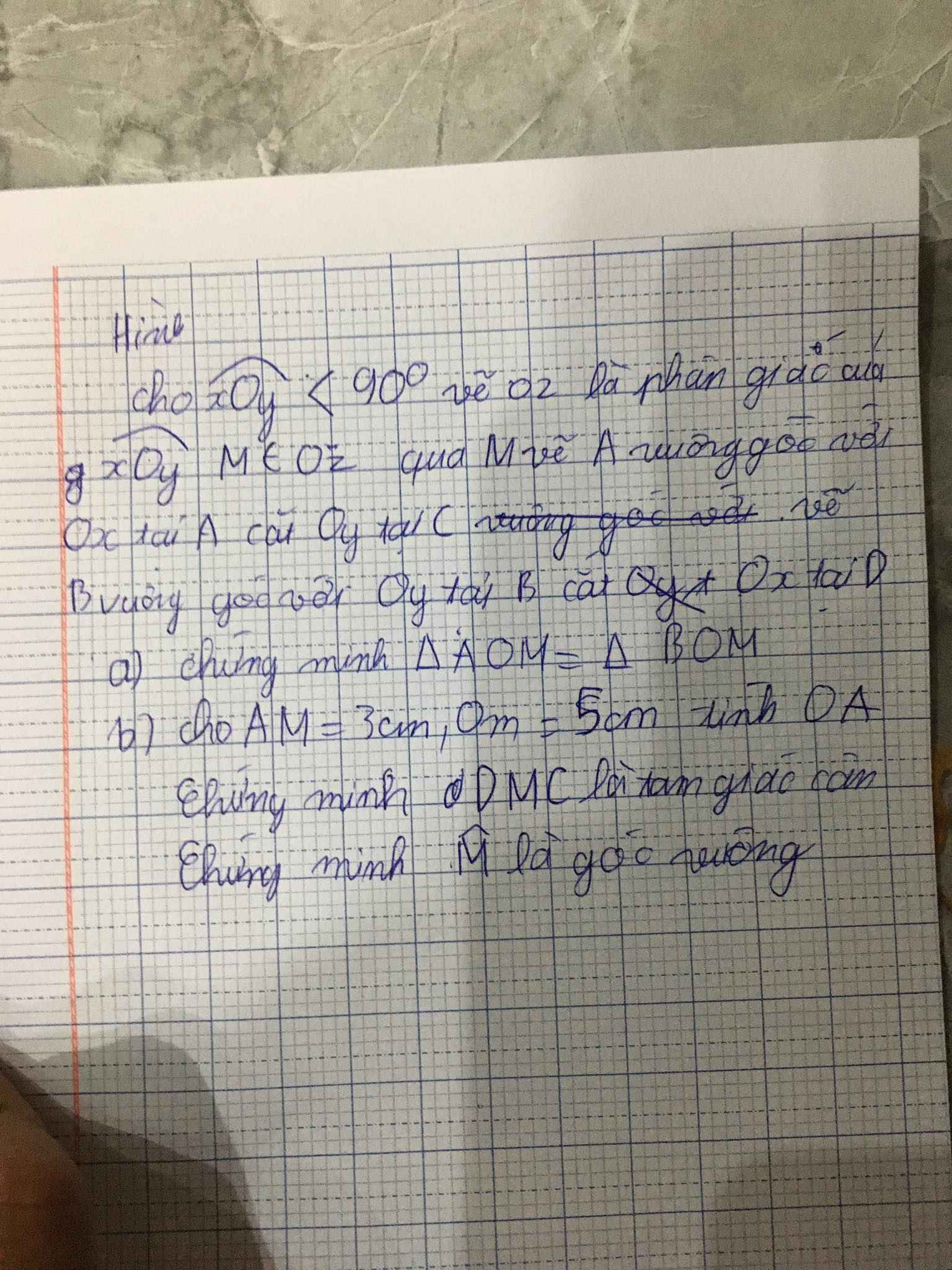


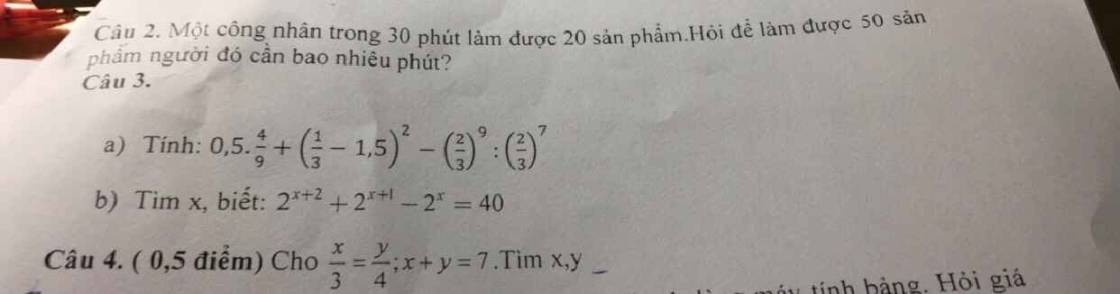 Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...
Hic... làm ơn giải giúp em câu nàyT-T nhanh giúp với nếu có thể giải thích dùm cảm ơn...




