16*:
a) Ta có:
\(VP=x^4-y^4\\
=\left(x^2-y^2\right)\left(x^2+y^2\right)\\
=\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)\\
=\left(x-y\right)\left[x\left(x^2+y^2\right)+y\left(x^2+y^2\right)\right]\\
=\left(x-y\right)\left(x^3+xy^2+x^2y+y^3\right)=VT\)
b) Ta có:
\(VP=x^5+y^5\\ =\left(x^5+x^4y\right)+\left(xy^4+y^5\right)-\left(x^4y+xy^4\right)\\ =x^4\left(x+y\right)+y^4\left(x+y\right)-xy\left(x^3+y^3\right)\\ =\left(x+y\right)\left(x^4+y^4\right)-xy\left(x+y\right)\left(x^2-xy+y^2\right)\\ =\left(x+y\right)\left[\left(x^4+y^4\right)-xy\left(x^2-xy+y^2\right)\right]\\ =\left(x+y\right)\left(x^4-x^3y+x^2y^2-xy^3+y^4\right)=VT\)
14:
a: \(4x\left(x-5\right)-\left(x-1\right)\left(4x-3\right)=5\)
=>\(4x^2-20x-\left(4x^2-7x+3\right)=5\)
=>\(4x^2-20x-4x^2+7x-3=5\)
=>-13x=8
=>\(x=-\dfrac{8}{13}\)
b: \(\left(x+3\right)\left(4-x\right)+\left(x-1\right)\left(x+1\right)=10\)
=>\(4x-x^2+12-3x+x^2-1=10\)
=>x+11=10
=>x=-1
c: \(-4x^2\left(x-7\right)+4x\left(x^2-5\right)=28x^2-13\)
=>\(28x^2-13=-4x^3+28x^2+4x^3-20x=28x^2-20x\)
=>20x=13
=>\(x=\dfrac{13}{20}\)
15:
a: \(A=\left(x-5\right)\left(2x+3\right)-2x\left(x-3\right)+x+7\)
\(=2x^2+3x-10x-15-2x^2+6x+x+7\)
=-8
b: \(B=4\left(y-6\right)-y^2\left(3y+2\right)+y\left(5y-4\right)+3y^2\left(y-1\right)\)
\(=4y-24-3y^3-2y^2+5y^2-4y+3y^3-3y^2\)
=-24

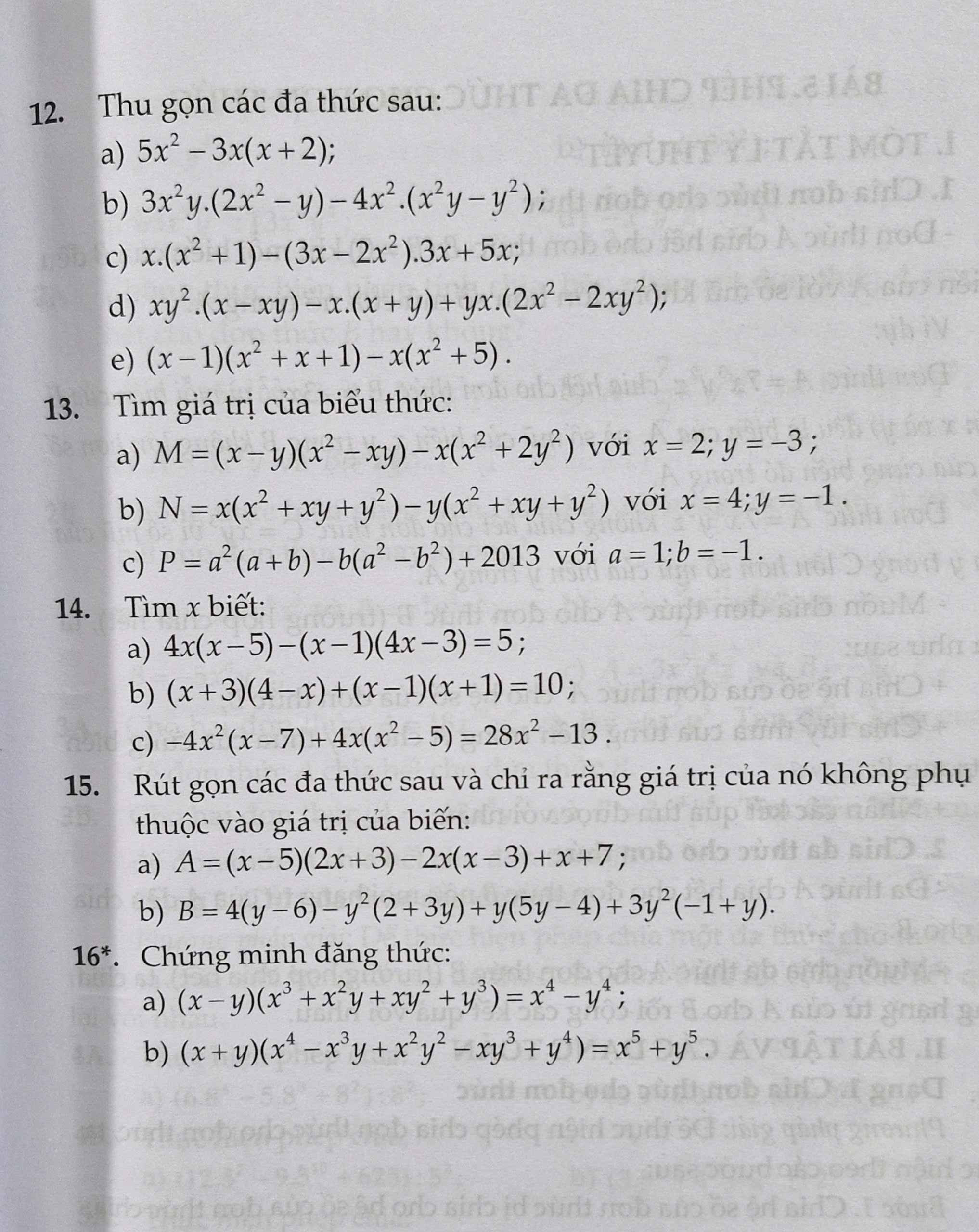





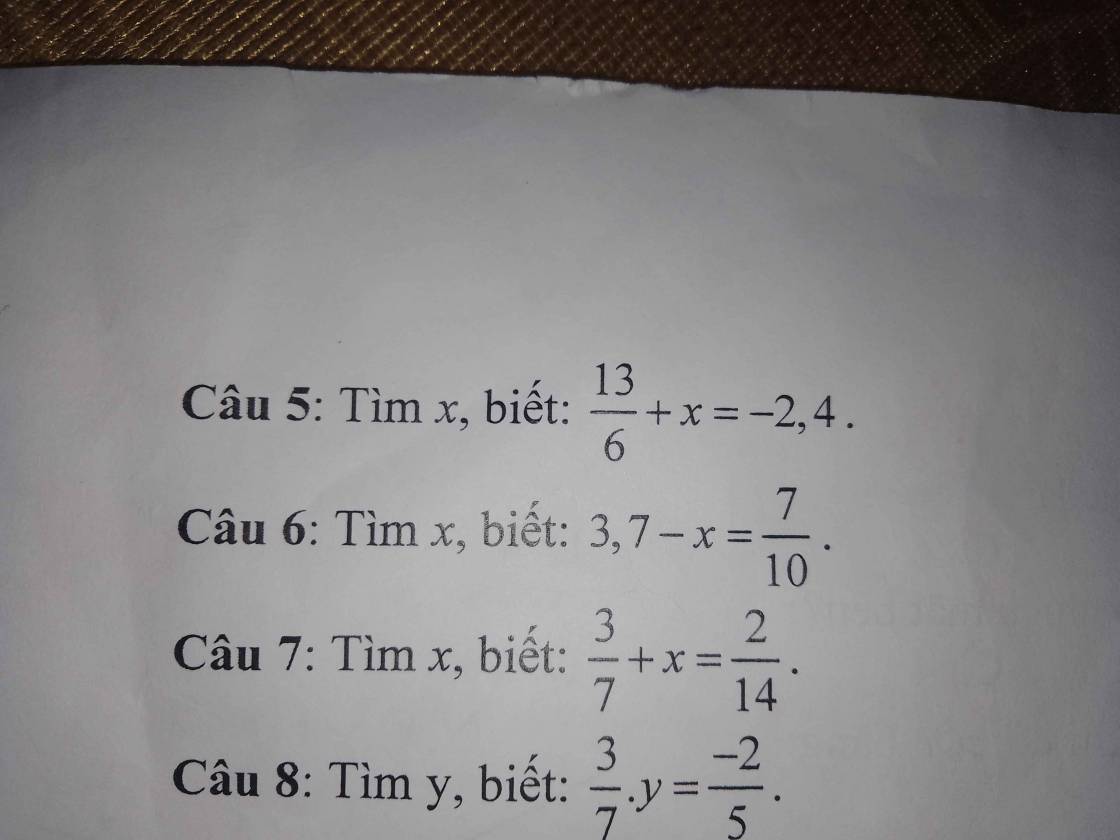



 giải giúp em với ạ
giải giúp em với ạ 
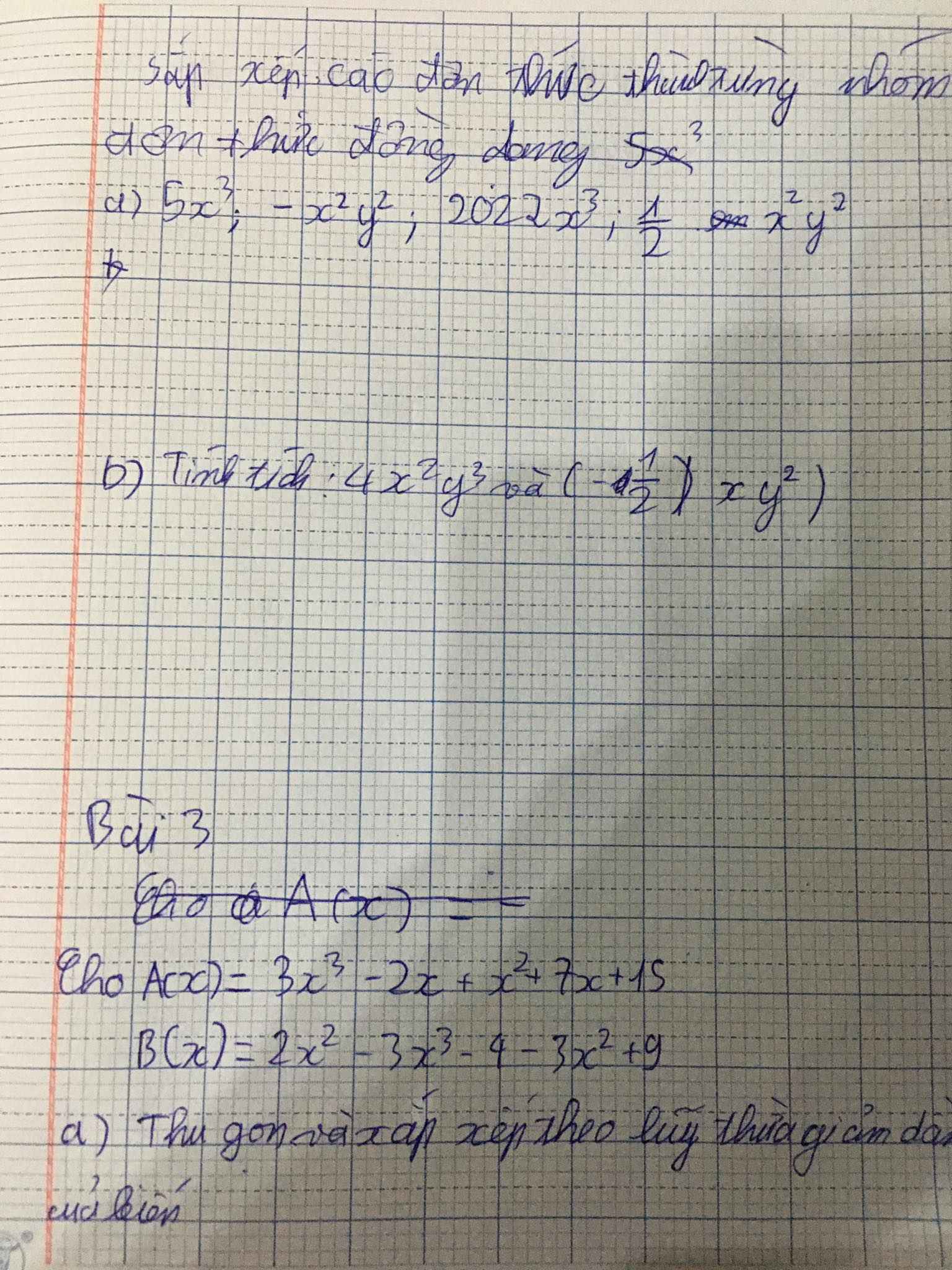

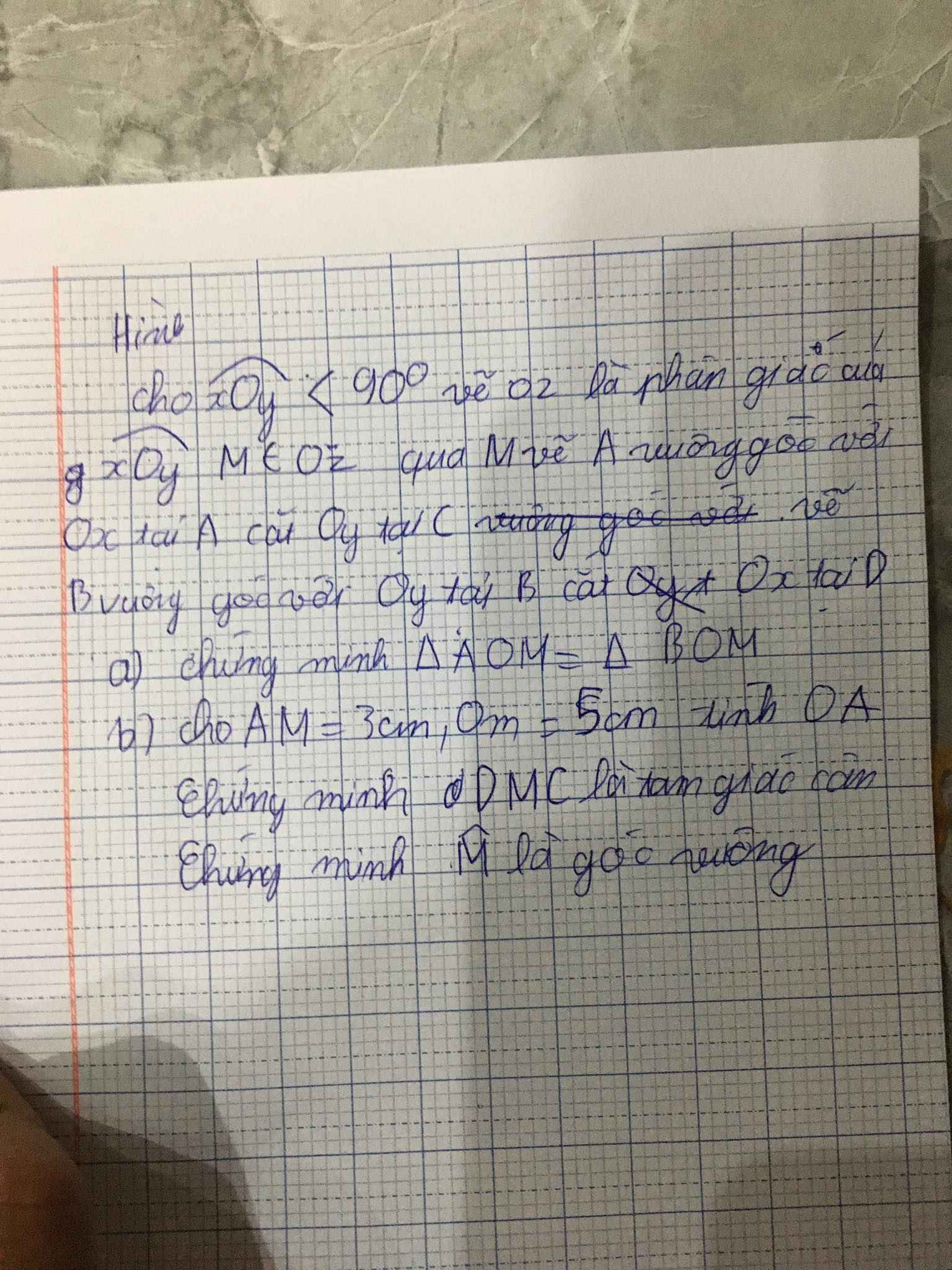

 ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ
ai giải giúp em từ 3 đến bài 12 với ạ em đang cần gấp chiều em đi thi ạ










