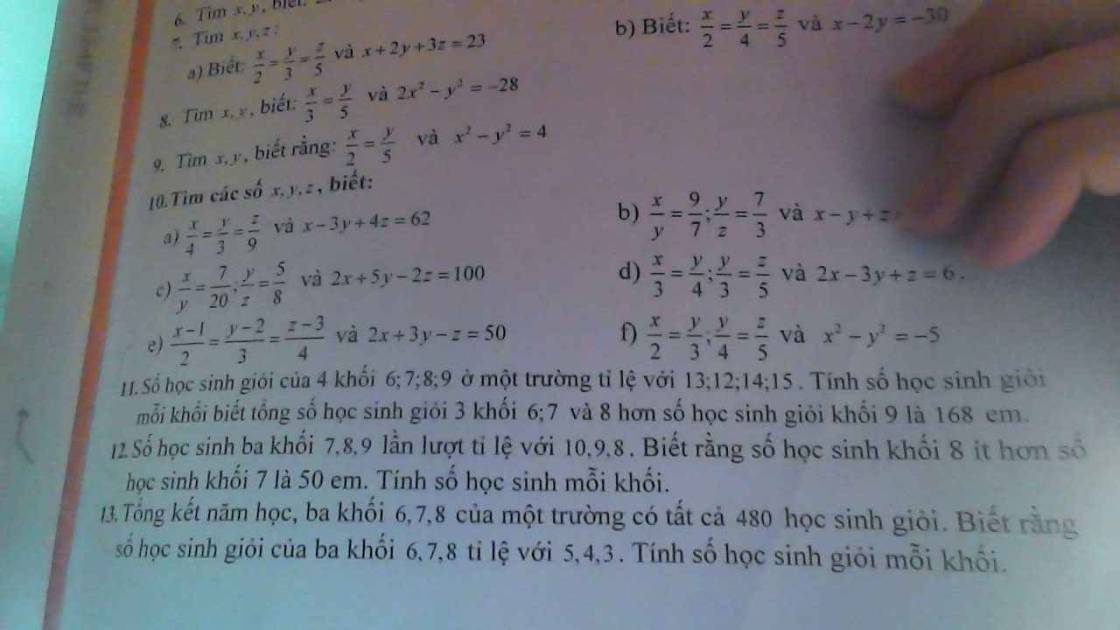Bài 14
\(A+B+C=4x^2-5xy+3y^2+3x^2+2xy+y^2-x^2+3xy+2y^2\)
\(=\left(4x^2+3x^2-x^2\right)+\left(-5xy+2xy+3xy\right)+\left(3y^2+y^2+2y^2\right)\)
\(=6x^2+6y^2=6\left(x^2+y^2\right)\)
\(B-C-A=\left(3x^2+2xy+y^2\right)-\left(-x^2+3xy+2y^2\right)-\left(4x^2-5xy+3y^2\right)\)
\(=3x^2+2xy+y^2+x^2-3xy-2y^2-4x^2+5xy-3y^2\)
\(=\left(3x^2+x^2-4x^2\right)+\left(2xy-3xy+5xy\right)+\left(y^2-2y^2-3y^2\right)\)
\(=4xy+-4y^2=4y\left(x-y\right)\)
\(2A-3B-C=2\left(4x^2-5xy+3y^2\right)-3\left(3x^2+2xy+y^2\right)-\left(-x^2+3xy+2y^2\right)\)
\(=8x^2-10xy+6y^2-9x^2-6xy-3y^2+x^2-3xy-2y^2\)
\(=\left(8x^2-9x^2+x^2\right)+\left(-10xy-6xy-3xy\right)+\left(6y^2-3y^2-2y^2\right)\)
\(=-19xy+y^2=y\left(y-19x\right)\)
Bài 17 :
a) \(A=x^2-3xy-y^2+1\)
\(B=2x^2+y^2-7xy-5\)
\(\Rightarrow A+B=3x^2-10xy-4\)
b) \(A-B=-x^2-2y^2+4xy+6\)
\(C+A-B=0\)
\(\Rightarrow C=-\left(A-B\right)\)
\(\Rightarrow C=-\left(-x^2-2y^2+4xy+6\right)\)
\(\Rightarrow C=x^2+2y^2-4xy-6\)
c) Với \(x=2;y=-\dfrac{1}{2}\)
\(C=2^2+2\left(-\dfrac{1}{2}\right)^2-4.2.\left(-\dfrac{1}{2}\right)-6=4+\dfrac{1}{2}+4-6=\dfrac{5}{2}\)
Bài 18
\(P\left(x\right)+Q\left(x\right)-R\left(x\right)=5x^2+5x-4+2x^2-3x+1-\left(4x^2-x+3\right)\)
\(=5x^2+5x-4+2x^2-3x+1-4x^2+x-3\)
\(=\left(5x^2+2x^2-4x^2\right)+\left(5x-3x+x\right)+\left(-4+1-3\right)\)
\(=3x^2+3x-6=3\left(x^2+x-2\right)\)
\(x=\dfrac{-1}{2}\) thay vào đa thức trên ta có: \(3.\left[\left(\dfrac{1}{2}\right)^2-\dfrac{1}{2}-2\right]=3.\dfrac{-9}{4}=-\dfrac{27}{4}\)

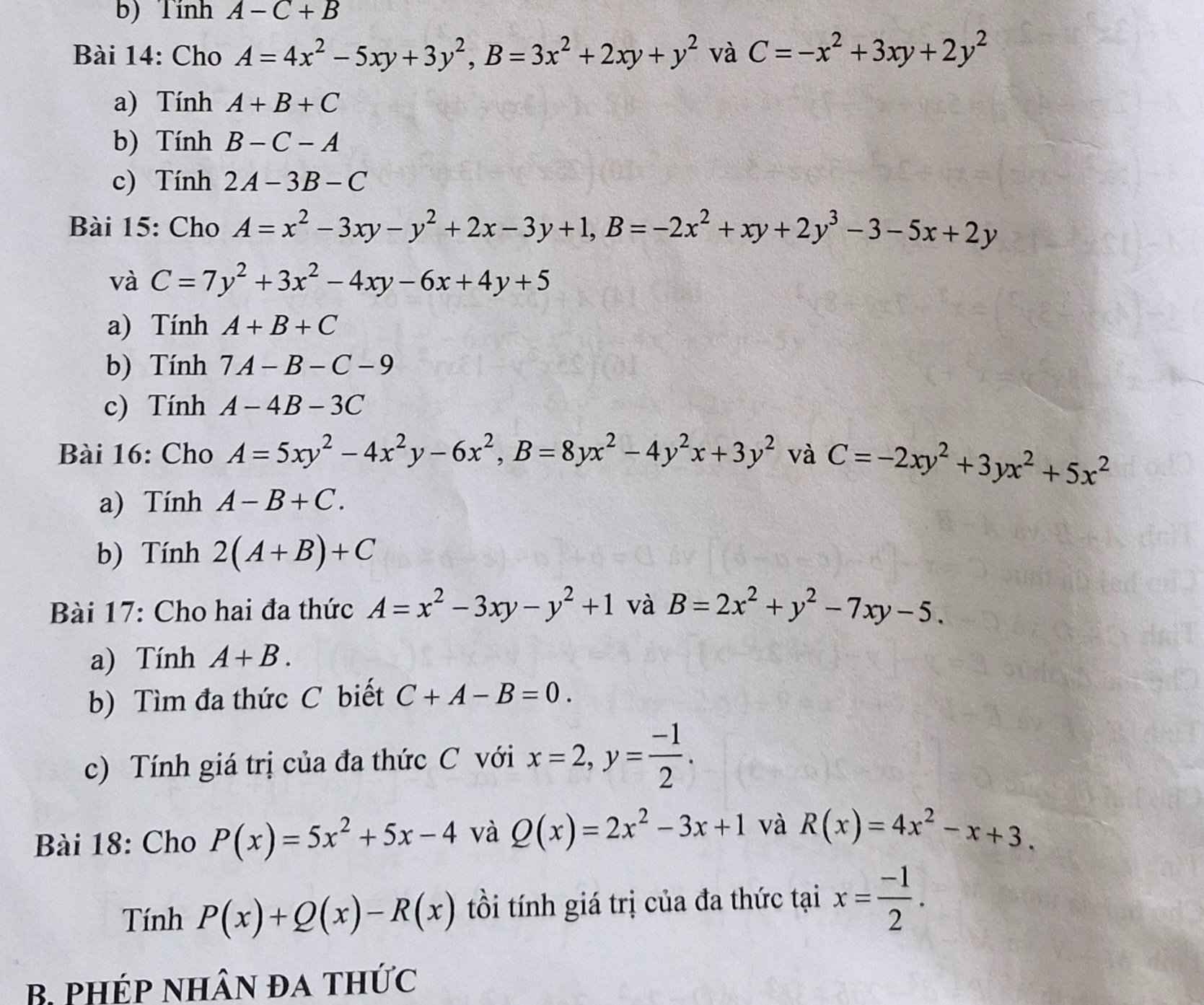











 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ

 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ