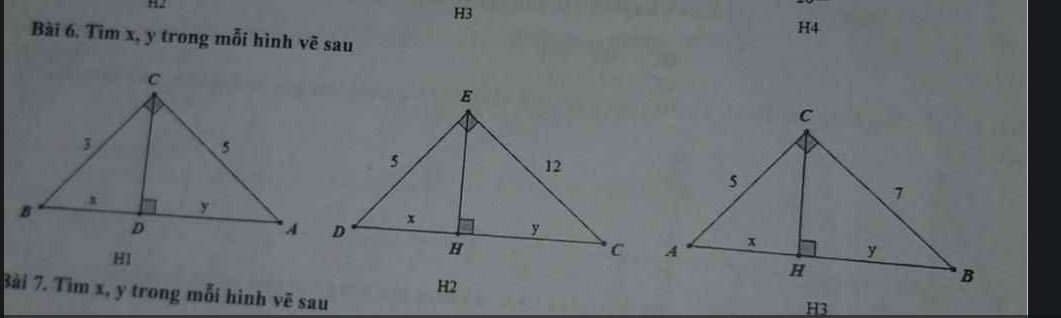
H1:
Xét \(\Delta ABC\) vuông tại C, CD là đường cao:
\(+)BC^2+AC^2=BA^2\left(Pytago\right).\\ \Rightarrow3^2+5^2=BC^2.\\ \Rightarrow BA=\sqrt{3^2+5^2}=\sqrt{34}\left(đvđd\right).\)
\(+)AC^2=AD.BA.\\ \Rightarrow5^2=y.\sqrt{34}.\\ \Leftrightarrow y=\dfrac{25\sqrt{34}}{34}\left(đvđd\right).\)
\(BD=BA-AD=\sqrt{34}-\dfrac{25\sqrt{34}}{34}=\dfrac{9\sqrt{34}}{34}.\\ \Rightarrow x=\dfrac{9\sqrt{34}}{34}\left(đvđd\right).\)
H2:
Xét \(\Delta EDC\) vuông tại E, EH là đường cao:
\(+)DC^2=ED^2+EC^2\left(Pytago\right).\\ \Rightarrow DC^2=5^2+12^2.\Rightarrow DC=\sqrt{5^2+12^2}=13\left(đvđd\right).\)
\(+)EC^2=HC.DC.\\ \Rightarrow12^2=y.13.\\ \Leftrightarrow y=\dfrac{144}{13}\left(đvđd\right).\)
\(DH=DC-HC=13-\dfrac{144}{13}=\dfrac{25}{13}.\\ \Rightarrow x=\dfrac{25}{13}\left(đvđd\right).\)
H3:
Xét \(\Delta CAB\) vuông tại C, CH là đường cao:
\(+)AB^2=BC^2+AC^2\left(Pytago\right).\\ \Rightarrow AB^2=7^2+5^2.\Rightarrow AB=\sqrt{7^2+5^2}=\sqrt{74}\left(đvđd\right).\)
\(+)BC^2=BH.BA.\\ \Rightarrow7^2=y.\sqrt{74}.\\ \Leftrightarrow y=\dfrac{49\sqrt{74}}{74}\left(đvđd\right).\)
\(AH=AB-HB=\sqrt{74}-\dfrac{49\sqrt{74}}{74}=\dfrac{25\sqrt{74}}{74}.\\ \Rightarrow x=\dfrac{25\sqrt{74}}{74}\left(đvđd\right).\)
Xét ΔABCΔABC vuông tại C, CD là đường cao:
+)BC2+AC2=BA2(Pytago).⇒32+52=BC2.⇒BA=√32+52=√34(đvđd).+)BC2+AC2=BA2(Pytago).⇒32+52=BC2.⇒BA=32+52=34(đvđd).