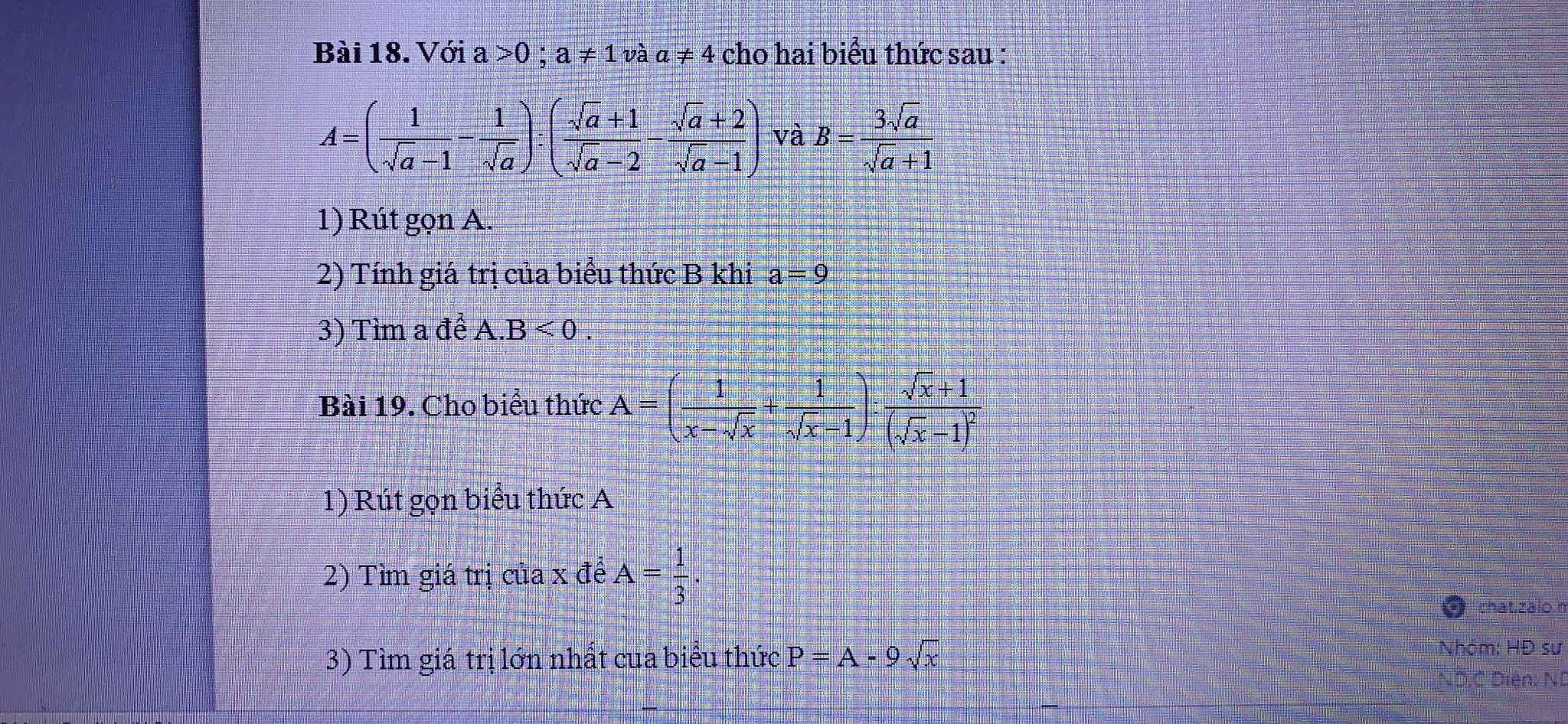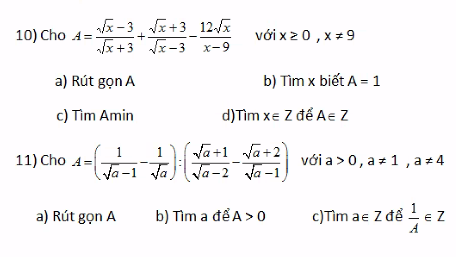Bài 18
a, Với \(a>0;a\ne1;4\)
\(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\left(\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b, Thay a = 9 => căn a = 3
\(A=\dfrac{3-2}{3.3}=\dfrac{1}{9}\)
c, Ta có : \(A.B=\dfrac{\sqrt{a}-2}{3\sqrt{a}}.\dfrac{3\sqrt{a}}{\sqrt{a}+1}=\dfrac{\sqrt{a}-2}{\sqrt{a}+1}< 0\)
Vì \(\sqrt{a}+1>\sqrt{a}-2\)
\(\left\{{}\begin{matrix}\sqrt{a}+1>0\\\sqrt{a}-2< 0\end{matrix}\right.\Leftrightarrow a< 4\)
Kết hợp với đk vậy \(0< a< 4;a\ne1\)
Bài 18:
1) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
2) Thay a=9 vào B, ta được:
\(B=\dfrac{3\cdot3}{3+1}=\dfrac{9}{4}\)
Bài 19:
1) Ta có: \(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)