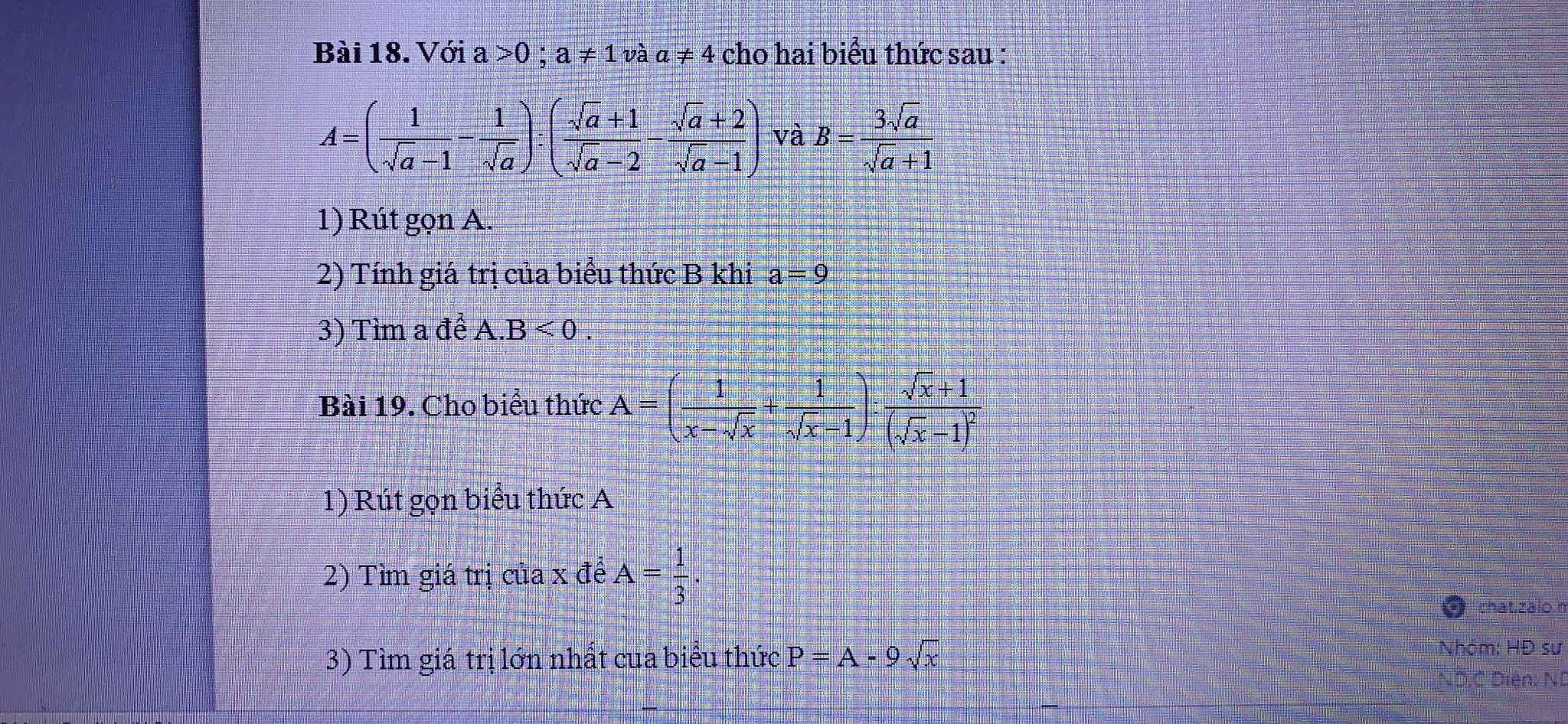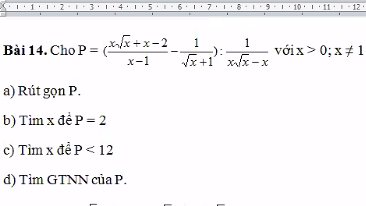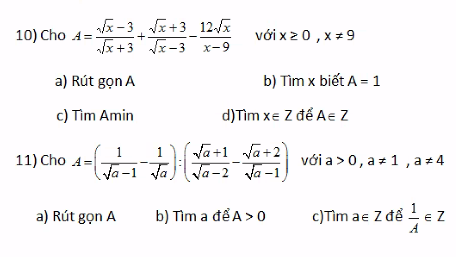a, \(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)ĐK : \(x>0;x\ne1\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
b, \(A=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}=\dfrac{1}{3}\Rightarrow3\sqrt{x}-3=\sqrt{x}\Leftrightarrow2\sqrt{x}=3\)
\(\Leftrightarrow\sqrt{x}=\dfrac{3}{2}\Leftrightarrow x=\dfrac{9}{4}\)
c, \(P=\dfrac{\sqrt{x}-1}{\sqrt{x}}-9\sqrt{x}=\dfrac{\sqrt{x}-1-9x}{\sqrt{x}}\)
\(=1-\dfrac{1}{\sqrt{x}}-9\sqrt{x}\)Đặt \(\sqrt{x}=t^2\left(t>0\right)\)
\(1-t-9t^2=-\left(9t^2-t-1\right)=-\left(9t^2-2.3.\dfrac{1}{6}.t+\dfrac{1}{36}-\dfrac{37}{36}\right)\)
\(=-\left(3t-\dfrac{1}{6}\right)+\dfrac{37}{36}\le\dfrac{37}{36}\)
Dấu ''='' xảy ra khi t = 1/18 => t^2 = 1/324 => \(\sqrt{x}=\dfrac{1}{324}\Rightarrow x=\dfrac{1}{104876}\)
Vậy GTLN P là 37/36 khi x = 1/104876
\(\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)=\(\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
1) Ta có: \(A=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
2) Để \(A=\dfrac{1}{3}\) thì \(\dfrac{\left(\sqrt{x}-1\right)}{\sqrt{x}}=\dfrac{1}{3}\)
\(\Leftrightarrow3\sqrt{x}-3-\sqrt{x}=0\)
\(\Leftrightarrow2\sqrt{x}=3\)
hay \(x=\dfrac{9}{4}\)(thỏa ĐK)