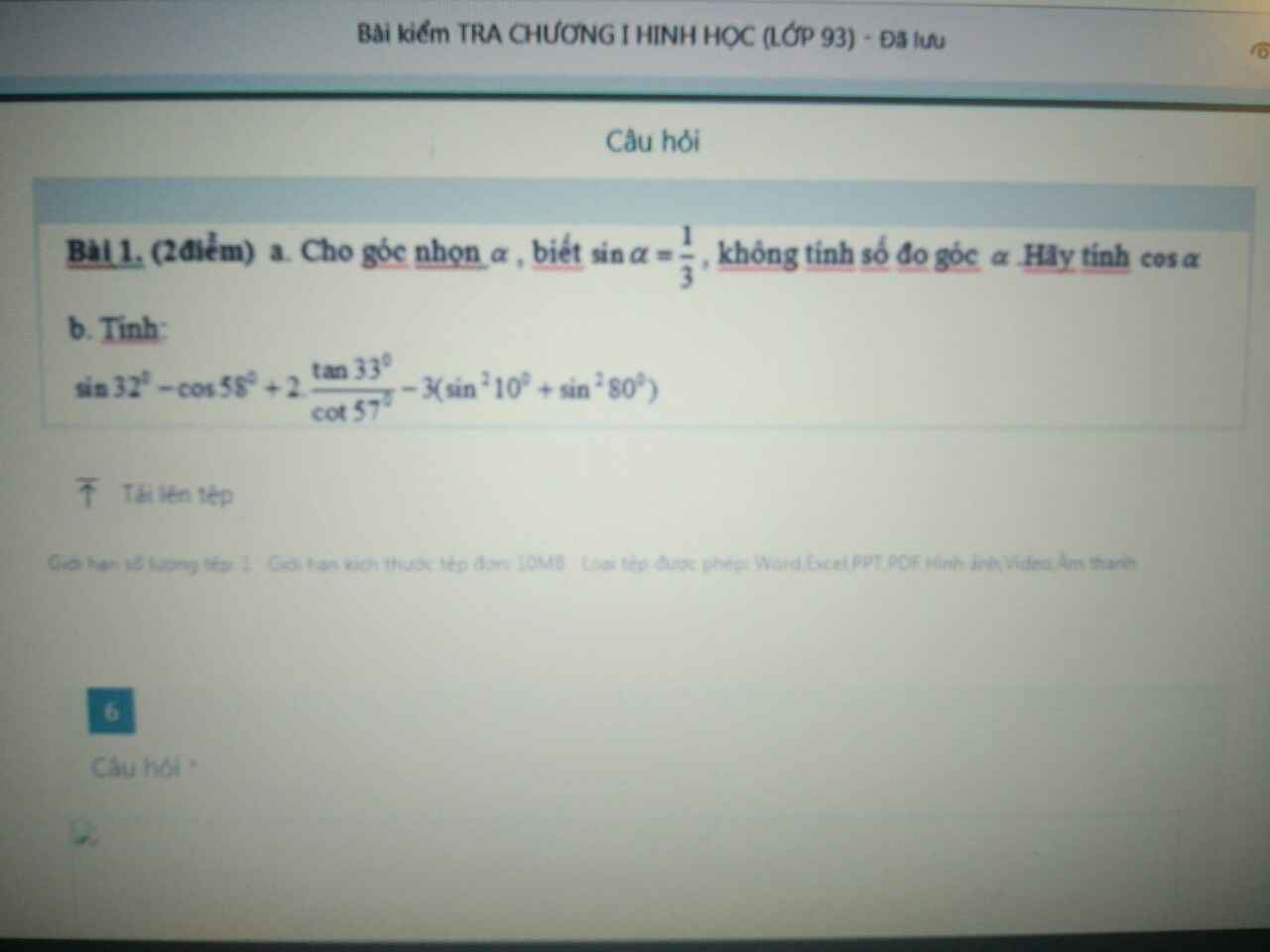
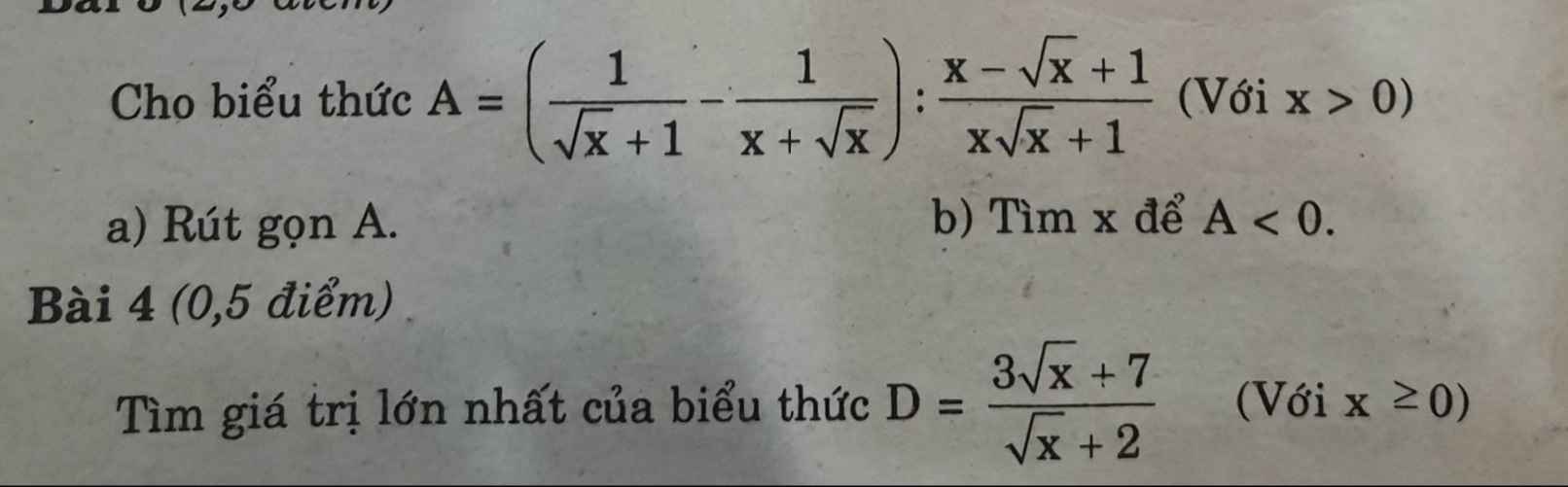a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{x+\sqrt{x}}\right):\dfrac{x-\sqrt{x}+1}{x\sqrt{x}+1}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{x-1}{\sqrt{x}}\)
b: Để A<0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: 0<x<1
với \(x\ge0\) ta có :\(D=\dfrac{3\sqrt{x+7}}{\sqrt{x}+2}=\dfrac{3\left(\sqrt{x}+2\right)+1}{\sqrt{x}+2}=3+\dfrac{1}{\sqrt{x}+2}\)
D lớn nhất \(\Leftrightarrow\sqrt{x}+2\) nhỏ nhất:
Mà:\(\sqrt{x}+2\ge2\)
vậy:\(\max\limits_D=3+\dfrac{1}{2}=\dfrac{7}{2}\Leftrightarrow x=0\)
D=3(căn x +2)/căn x +2 + 1/căn x +2
=3 + 1/ căn x +2 >=3
D lớn nhất khi 1/căn x + 2 lớn nhất
khi căn x + 2 >=2
khi căn x =0
suy ra x=0