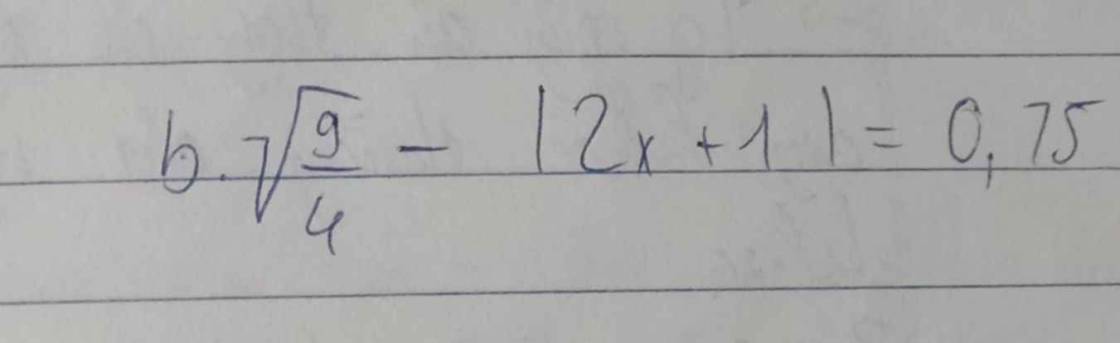Giải
\(\sqrt{\dfrac{9}{4}}-\left|2x+1\right|=0,75\)
TH1: \(\left|2x+1\right|=2x+1\)
\(=>\sqrt{\dfrac{9}{4}}-\left(2x+1\right)=0,75\\ =>\dfrac{3}{2}-2x-1=\dfrac{3}{4}\\ =>\left(\dfrac{3}{2}-1\right)-2x=\dfrac{3}{4}\\ =>\dfrac{1}{2}-2x=\dfrac{3}{4}\\ =>2x=\dfrac{1}{2}-\dfrac{3}{4}\\ =>2x=-\dfrac{1}{4}\\ =>x=\left(-\dfrac{1}{4}\right):2\\ =>x=-\dfrac{1}{8}\)
\(TH2:\left|2x+1\right|=-2x-1\\ =>\sqrt{\dfrac{9}{4}}-\left(-2x-1\right)=\dfrac{3}{4}\\ =>\dfrac{3}{2}+2x+1=\dfrac{3}{4}\\ =>\left(\dfrac{3}{2}+1\right)+2x=\dfrac{3}{4}\\ =>\dfrac{5}{2}+2x=\dfrac{3}{4}\\ =>2x=\dfrac{3}{4}-\dfrac{5}{2}\\ =>2x=-\dfrac{7}{4}\\ =>x=\left(-\dfrac{7}{4}\right):2\\ =>x=-\dfrac{7}{8}\)