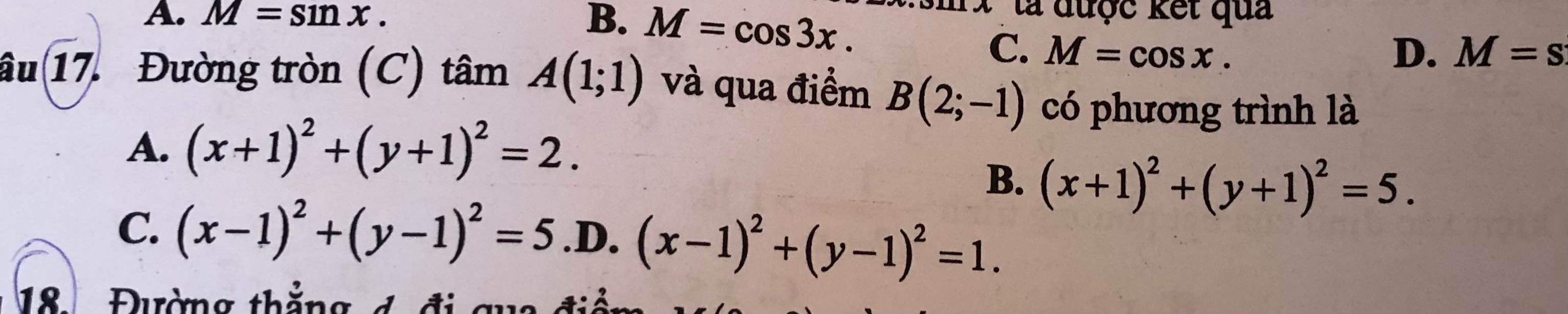Question

Giải chi tiết giúp mình nhé

Answer 1

Câu 5: 

a: Đúng

b: Xét ΔABC có \(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)

=>\(cosA=\dfrac{85^2+54^2-52,1^2}{2\cdot85\cdot54}\simeq0,81\)

=>\(\widehat{A}\simeq36^0\)

=>Sai

c: \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\dfrac{54^2+52,1^2-85^2}{2\cdot54\cdot52,1}\simeq-0,28\)

=>\(\widehat{B}\simeq106^0\)

=>Sai

d: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

=>\(\widehat{C}=180^0-36^0-106^0=38^0\)

=>Đúng

Câu 6:

a:Xét ΔABC có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)

=>\(cosC=\dfrac{b^2+a^2-c^2}{2ba}\)

=>\(b^2+a^2-c^2=2ab\cdot cosC\)

=>\(c^2=a^2+b^2-2ab\cdot cosC\)

=>Đúng

b: \(c^2=a^2+b^2-2ab\cdot cosC\)

=>\(c^2=49,4^2+26,4^2-2\cdot49,4\cdot26,4\cdot cos47^020'\)

=>\(c\simeq37\left(cm\right)\)

=>Sai

c: Xét ΔABC có \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\)

=>\(sinA=\dfrac{BC\cdot sinC}{AB}=\dfrac{49,4\cdot sin47^020'}{37}\simeq0,98\)

=>\(\widehat{A}\simeq79^0\)

=>Sai

d: Xét ΔABC có \(\widehat{A}+\widehat{C}+\widehat{B}=180^0\)

=>\(\widehat{B}=180^0-79^0-47^020'\simeq53^040'\)

=>Sai