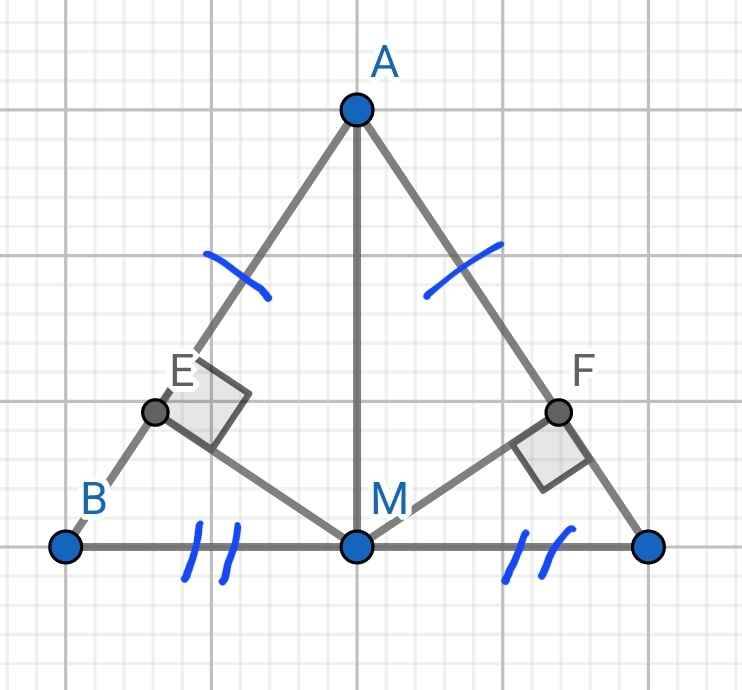
a) Xét ∆ABM và ∆ACM có:
AB = AC (∆ABC cân tại A)
BM = CM (AM là trung tuyến)
AM chung
⇒ ∆ABM = ∆ACM (c-c-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ ∠BAM = ∠CAM (hai góc tương ứng)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AEM và ∆AFM có:
AM chung
∠EAM = ∠FAM (cmt)
⇒ ∆AEM = ∆AFM (cạnh huyền - góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)







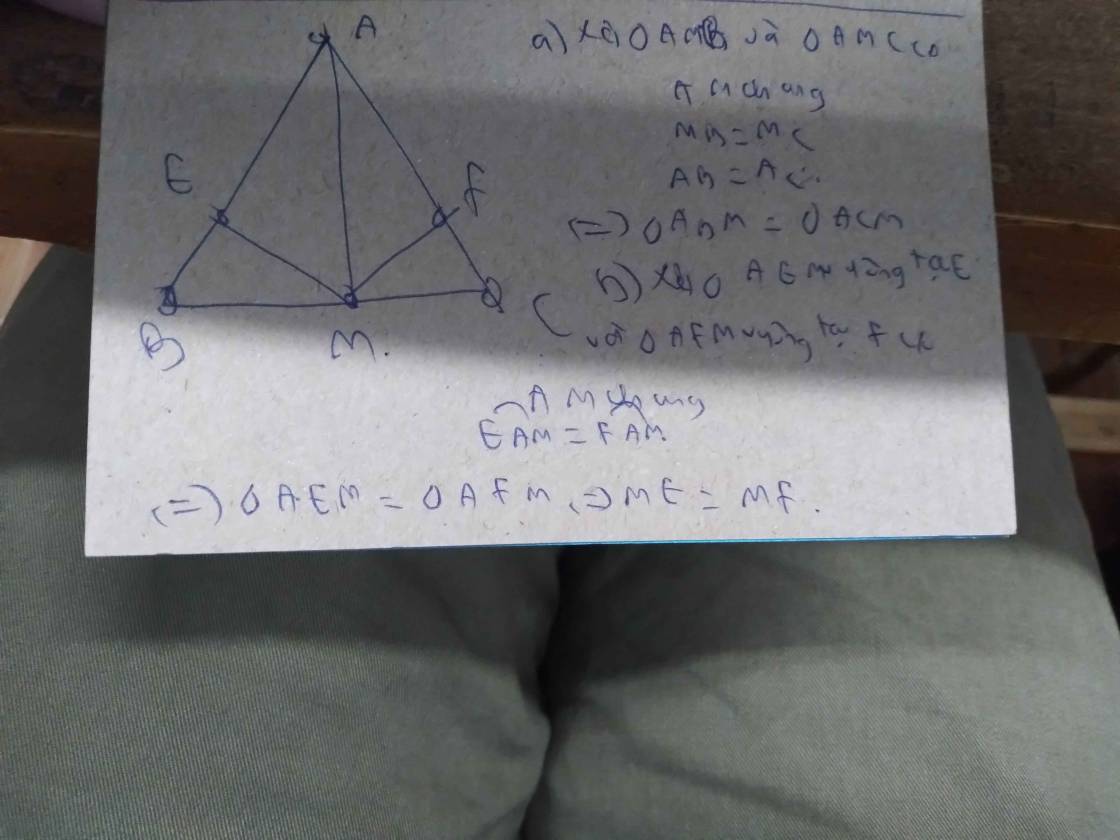




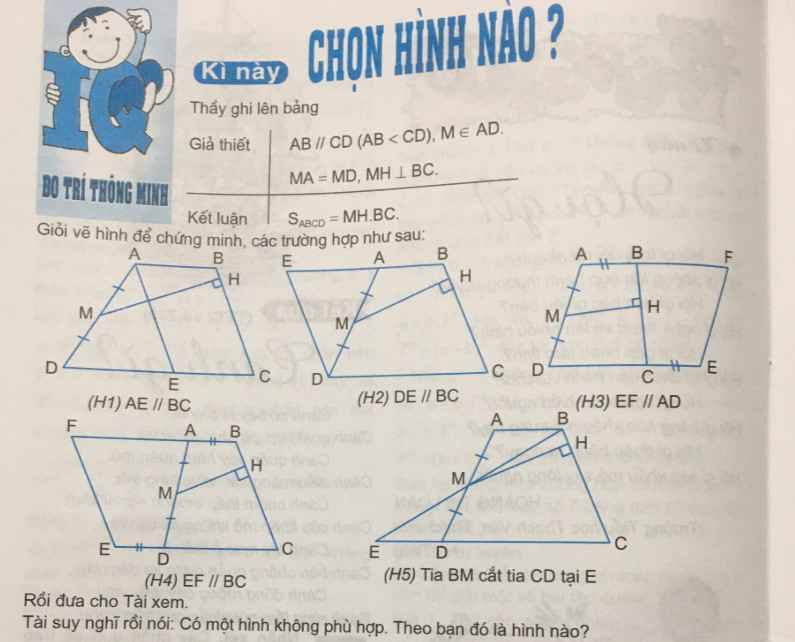




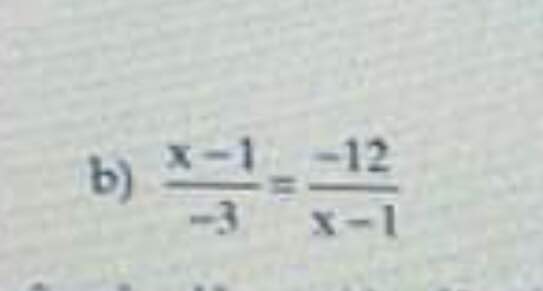


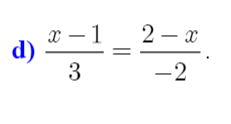

 giải chi tiết hộ mik với ạ
giải chi tiết hộ mik với ạ


