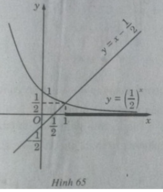
Vẽ đồ thị của hàm số 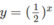 và đường thẳng
và đường thẳng 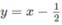 trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số 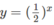 nằm phía dưới đường thẳng
nằm phía dưới đường thẳng 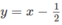 . Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)
. Vậy tập nghiệm của bất phương trình đã cho là (1;+
∞
)