ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
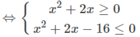
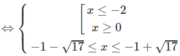
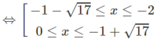
Vậy tập nghiệm là
![]()
ln|(x − 2)(x + 4)| ≤ ln8
⇔| x 2 + 2x − 8| ≤ 8
⇔ −8 ≤ x 2 + 2x – 8 ≤ 8
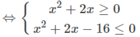
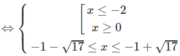
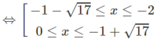
Vậy tập nghiệm là
![]()
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
Giải các bất phương trình sau: (2x − 7)ln(x + 1) > 0
Giải các phương trình sau: ln(4x + 2) - ln(x - 1) = lnx
Giải các bất phương trình lôgarit sau: log x 2 - x - 2 < 2 log 3 - x
Giải bất phương trình ln (1 + x)< x ?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Giải các bất phương trình lôgarit sau:
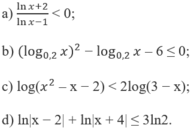
Bất phương trình ln(2x2 + 3) > ln(x2 + ax + 1) nghiệm đúng với mọi số thực x khi:
A. - 2 2 < a < 2 2
B. 0 < a < 2 2
C. 0 < a < 2
D. - 2 < a < 2
Giải bất phương trình l n ( x x - 2 x - 2 ) < 0
A. -1 ≥ x ≥ 3
B. - 1 - 3 < x < 1 + 3
C. x ∞ - 1 ; 1 - 3 ) ∪ ( 1 + 3 )
D. x ∞ ( 1 + 3 ) , 3
Giải các bất phương trình lôgarit sau: log 0 , 2 x 2 - log 0 , 2 x - 6 ≤ 0