
- Tính giá trị của hàm số tại các điểm trên (cả hai đầu mút) và so sánh.
Cách giải:
Ta có:
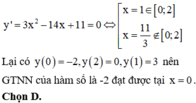

- Tính giá trị của hàm số tại các điểm trên (cả hai đầu mút) và so sánh.
Cách giải:
Ta có:
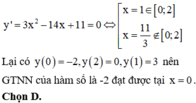
Giá trị nhỏ nhất của hàm số y = − x + 1 2 x + 3 trên đoạn [0;2] là:
A. 2
B. 1 3
C. − 1 7
D. 0
Giá trị nhỏ nhất của hàm số y = − x + 1 2 x + 3 trên đoạn 0 ; 2 là
A. 1 3
B. - 1 7
C. 2
D. 0
Ký hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn [ 0;2]. Giá trị a+ A bằng
A. 7
B. 18
C. 0
D. 12
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Kí hiệu a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x 2 + x + 4 x + 1 trên đoạn 0 ; 2 . Khi đó giá trị của a + A bằng:
A. 7
B. 18
C. 0
D. 12
Giá trị nhỏ nhất của hàm số y = x + e 2 x trên đoạn 0 ; 2 là
A. 0
B. 1
C. 1 + 2 e 2
D. 1 + e 2
Cho hàm số f ( x ) = a x 4 + b x 2 + c có m i n ( - ∞ ; 0 ) f ( x ) = f ( - 1 ) . Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [ 1 2 ;2] bằng
A. c + 8a
B. c - 7 16 a
C. c + 9 16 a
D. c - a
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) = - 2 x 4 + 4 x 2 + 3 trên đoạn [0;2] lần lượt là
A. 6 và -12
B. 6 và -13
C. 5 và -13
D. 6 và -31
Giá trị nhỏ nhất của hàm số y = e x x 2 − x − 1 trên đoạn [0;2] là?
A. -e
B. -1
C. -2e
D. e 2