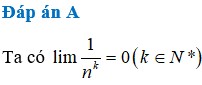Các câu hỏi tương tự
Trong không gian Oxyz, cho hình bình hành ABCD với A(1; 2; 3), B(5; 0; -1), C(4; 3; 6) và D(a;b;c) Giá trị của a+b+c bằng
A. 3
B. 11
C. 15
D. 5
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
−
6
x
+
9
và 2 đường thẳng x 0, y 0. Đường thẳng (d) có hệ số k (
k
∈
ℝ
) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là: A.
−
16
9...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
−
6
x
+
9
và 2 đường thẳng x 0, y 0. Đường thẳng (d) có hệ số k (
k
∈
ℝ
) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là: A.
−...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số:
y
x
2
−
6
x
+
9
và 2 đường thẳng x 0, y 0. Đường thẳng (d) có hệ số k (
k
∈
ℝ
) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là: A.
−
16
9...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Giá trị của l i m 1 n k ( k ∈ N * ) bằng.
A. 0
B. 2
C. 4
D. 5
Xét n là số nguyên dương và
1
+
x
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
k
x
k
+
.
.
....
Đọc tiếp
Xét n là số nguyên dương và 1 + x n = a 0 + a 1 x + a 2 x 2 + . . . + a k x k + . . . + a n x n . Biết rằng tồn tại số nguyên k , 1 ≤ k ≤ n - 1 , sao cho a k - 1 2 = a k 9 = a k + 1 24 . Giá trị của a 2 bằng
A. 66
B. 36
C. 55
D. 45
Cho hàm số
y
x
3
-
3
x
có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng
d
:
y
k
(
x
+
1
)
+
2
cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M (-1;2), tính tích tất cả các phần tử của tập S A....
Đọc tiếp
Cho hàm số y = x 3 - 3 x có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng d : y = k ( x + 1 ) + 2 cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M (-1;2), tính tích tất cả các phần tử của tập S
A. 1 9
B. - 2 9
C. 1 3
D. -1
Cho tập hợp A gồm n phần tử (
n
≥
4
) , biết rằng số tập con gồm 4 phần tử của A bằng 20 lần số tập con gồm 2 phần tử của A. Tìm k (
1
≤
k
≤
n
) sao cho số tập con gồm k phần tử của A lớn nhất A. k 9 B. k 7 C. k 8 D. k 6
Đọc tiếp
Cho tập hợp A gồm n phần tử ( n ≥ 4 ) , biết rằng số tập con gồm 4 phần tử của A bằng 20 lần số tập con gồm 2 phần tử của A. Tìm k ( 1 ≤ k ≤ n ) sao cho số tập con gồm k phần tử của A lớn nhất
A. k = 9
B. k = 7
C. k = 8
D. k = 6
Trong không gian Oxyz, cho hình vuông ABCD có A(8; 0; 3),C(0; -4; -5) và
D
(
a
;
b
;
c
)
(
a
;
b
;
c
∈
ℤ
)
thuộc mặt phẳng (Oyz). Giá trị a + b + c bằng A. -3 B. -2 C. 2 D. 3
Đọc tiếp
Trong không gian Oxyz, cho hình vuông ABCD có A(8; 0; 3),C(0; -4; -5) và D ( a ; b ; c ) ( a ; b ; c ∈ ℤ ) thuộc mặt phẳng (Oyz). Giá trị a + b + c bằng
A. -3
B. -2
C. 2
D. 3