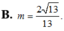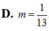Các câu hỏi tương tự
Cho số phức za+bi
a
,
b
∈
R
thỏa mãn
2
(
z
+
1
)
3
z
¯
+
i
(
5
-
i
)
. Giá trị Ha+2b bằng bao nhiêu?
Đọc tiếp
Cho số phức z=a+bi a , b ∈ R thỏa mãn 2 ( z + 1 ) = 3 z ¯ + i ( 5 - i ) . Giá trị H=a+2b bằng bao nhiêu?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai điểm A(1;-1;2),B(3;-4;-2)và đường thẳng
d
:
x
2
+
4
t
y
-
6
t...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(1;-1;2),B(3;-4;-2)và đường thẳng
d : x = 2 + 4 t y = - 6 t z = - 1 - 8 t . Điểm I(a,b,c) thuộc d là điểm thỏa mãn IA + IB đạt giá trị nhỏ nhất. Khi đó T = a + b + c bằng
A. 23 58
B. - 43 58
C. 65 29
D. - 21 58
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
![]()
![]()
![]()
![]()
Trong các số phức z thỏa mãn
12
-
5
i
z
+
17
+
17
i
z
-
2
-
i
13
....
Đọc tiếp
Trong các số phức z thỏa mãn 12 - 5 i z + 17 + 17 i z - 2 - i = 13 . Tìm giá trị nhỏ nhất của z .
A. 3 13 26
B. 5 5
C. 1 2
D. 2
Trong các số phức z thỏa mãn
(
12
-
5
i
)
z
+
17
+
7
i
z
-
2
-
i
13
. Tìm giá...
Đọc tiếp
Trong các số phức z thỏa mãn ( 12 - 5 i ) z + 17 + 7 i z - 2 - i = 13 . Tìm giá trị nhỏ nhất của z
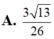
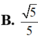
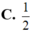
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
3
2
y
+
2
1
z
+
1
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 2 = y + 2 1 = z + 1 - 1 và mặt phẳng (P):x+y+z+2=0. Đường thẳng ∆ nằm trong mặt phẳng (P) vuông góc với đường thẳng d đồng thời khoảng cách từ giao điểm I của d với (P) đến ∆ bằng 42 . Gọi M(5;b;c) là hình chiếu vuông góc của I trên ∆ . Giá trị của bc bằng
A. -10
B. 10
C. 12
D. -20
Tính giá trị của biểu thức sau: \(log^2_{\dfrac{1}{a}}a^2+log_{a^2}a^{\dfrac{1}{2}}\) (1≠a>0)
A. \(\dfrac{17}{4}\)
B. \(\dfrac{13}{4}\)
C. \(-\dfrac{11}{4}\)
D. -\(\dfrac{15}{4}\)
Biết a b c,
∫
a
b
f
x
d
x
5
và
∫
c
b
f
x
d
x
3
. Tìm giá trị của
I
∫
a
c
f
x
d
x
. A. I 8 B. I 6 C. I 2 D. I 15
Đọc tiếp
Biết a < b < c, ∫ a b f x d x = 5 và ∫ c b f x d x = 3 . Tìm giá trị của I = ∫ a c f x d x .
A. I = 8
B. I = 6
C. I = 2
D. I = 15
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng
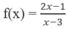
A. 1/3 và -3 B. 3/2 và -1
C. 2 và -3 D. 1/2 và 5
Cho số phức z thỏa mãn
z
-
2
+
i
+
z
+
1
-
i
13
Tìm giá trị nhỏ nhất m của biểu thức
z
+
2
-
i
Đọc tiếp
Cho số phức z thỏa mãn z - 2 + i + z + 1 - i = 13 Tìm giá trị nhỏ nhất m của biểu thức z + 2 - i
![]()