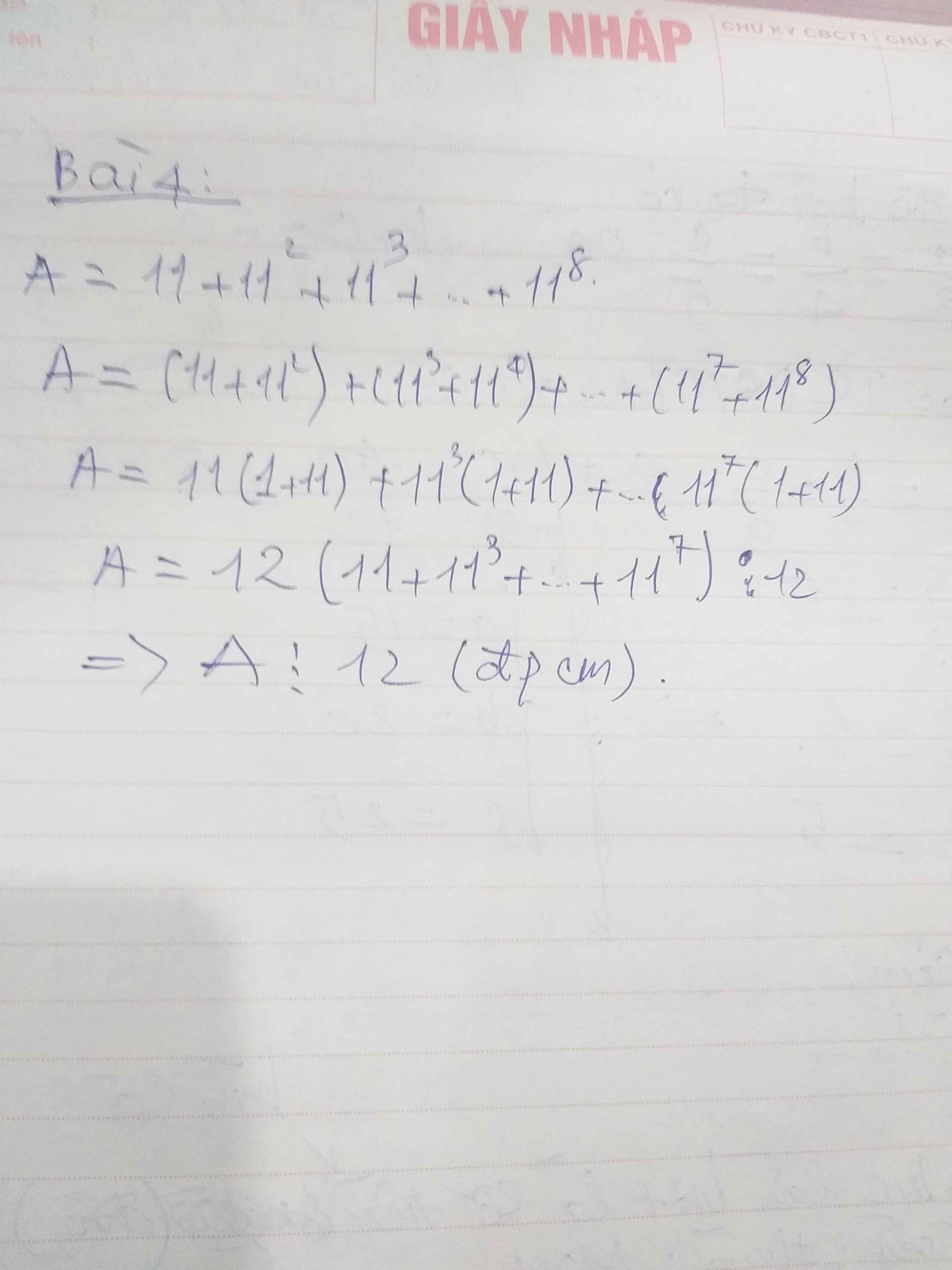Bài 3:
\(a,8^{10}-8^9-8^8\\ =8^8\cdot\left(8^2-8-1\right)\\ =8^8\cdot55⋮55\\ b,45^{45}\cdot15^{15}\\ =3^{45}\cdot15^{45}\cdot15^{15}\\ =3^{45}\cdot15^{60}\\ =3^{45}\cdot15^{30}\cdot15^{30}\\ =3^{45}\cdot15^{30}\cdot5^{30}\cdot3^{30}\\ =3^{75}\cdot75^{30}⋮75^{30}\\ c,24^{54}\cdot54^{24}\cdot2^{10}\\ =24^{54}\cdot27^{24}\cdot2^{24}\cdot2^{10}\\ =24^{54}\cdot3^{72}\cdot2^{34}\\ =72^{54}\cdot3^{18}\cdot2^{34}\\ =72^{54}\cdot\left(3^{18}\cdot2^{27}\right)\cdot2^7\\ =72^{54}\cdot72^9\cdot2^7\\ =72^{63}\cdot2^7⋮72^{63}\)
xem lại đề câu d
Bài 4:
\(A=11+11^2+11^3+...+11^8\\ A=11.\left(1+11\right)+11^3.\left(1+11\right)+...+11^7.\left(1+11\right)\\ A=11.12+11^3.12+...+11^7.12\\ A=12.\left(11+11^3+...+11^7\right)⋮12\)
Vậy...
Bài 5:
Ta có:
+) \(\overline{x183y}\) chia 2 dư 1 ⇒ \(y\in\left\{1,3,5,7,9\right\}\) (1)
+) \(\overline{x183y}\) chia 5 dư 1 ⇒ \(y\in\left\{1,6\right\}\) (2)
Từ (1) và (2) suy ra:
\(y=1\\ \Rightarrow\overline{x183y}=\overline{x1831}\)
Mặt khác:
\(\overline{x183y}\) chia 9 dư 1
\(\Rightarrow x+1+8+3+y=x+1+8+3+1=x+13\) chia 9 dư 1
\(\Rightarrow x=5\)
Vậy...